Low Density Parity Check (LDPC) Codes in 5G

5G networks uses low density parity check codes (ldpc) for forward error correction of shared channels used to communicate user data over air interface. These channel codes:

achieve channel capacity for large block lengths
extremely robust against noise
scalable and efficient hardware implementation.
Low power consumption and silicon footprint.
Can be enhanced to support diverse payload sizes and code-rates.
easy to design and implement the low complexity decoder.
capable of considering both reliability and high data rates.

The table of content of this tutorial is illustrated below:

Import Libraries
Symbol Mapping Configurations
Simulation for BER vs SNR
- BER vs SNR for fixed block-rate.
- BER vs SNR for fixed code rate.
LDPC Parameters
Performance Evaluation

Import Libraries

Python LIbraries

[1]:

import os
os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'

# %matplotlib widget
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes
from mpl_toolkits.axes_grid1.inset_locator import mark_inset

import numpy as np

5G Toolkit Libraries

[2]:

# import sys
# sys.path.append("../../../dist2/python3_11/")
import sys
sys.path.append("../../../")
from toolkit5G.SymbolMapping import Demapper
from toolkit5G.SymbolMapping import Mapper
from toolkit5G.ChannelCoder  import LDPCEncoder5G
from toolkit5G.ChannelCoder  import LDPCDecoder5G
from toolkit5G.ChannelCoder.LDPC  import LDPCparameters
from toolkit5G.Ratematcher.LDPC  import BitSelection
from toolkit5G.Ratematcher.LDPC  import BitDeselection

[3]:

# from IPython.display import display, HTML
# display(HTML("<style>.container { width:80% !important; }</style>"))

Symbol Mapping Configurations

Symbol mapping/Demapping is performed for:

QPSK constellation defined by constellation_type which encodes
1 bit per contellation symbol defined by num_bits_per_symbol.
The demapper generates log likelihood ratios configured by hard_out
using a Log-Map (“app”) decoder defined using demapping_method.

The flow of the implementation can be understood using folowing diagram: LDPCCodes

[4]:

constellation_type  = "qam"
num_bits_per_symbol = 2
hard_out            = False
demapping_method    = "app"

mapper  = Mapper(constellation_type, num_bits_per_symbol)
demapper= Demapper(demapping_method, constellation_type,  num_bits_per_symbol, hard_out = hard_out)

Simulation: Variation in Reliability with code-rate for fixed block-length

LDPC Parameters

tbSize: Defines the transport block size to be processed by LDPC Channel coder.
codeRate: codeRate of LDPC codec.
lpdcConfig: LDPC configuration is used to generate the LDPC parameters. as described below.
k: Number of information bits to be encoded.
bg: Base graph type.
zc: Lifting factor size.
numCBs: Number of codeblocks.

Note: tbSize and block length are different in LDPC codes. The length of block encoded using LDPC is given by K.

Simulation Procedure

This subsection performs the simulation which involve following steps:

Computation of LDPC parameters based on tbSize and codeRate.
Bits tensor generation of dimension numBatches \(\times\) numCBs \(\times\) k.
LDPC Encoding.
Rate matching
- Bit-Selection
- Bit-Interleaving
QPSK Symbol Mapping of encoded bits.
Passing through the AWGN Channel
- Adding noise to BPSK symbols with a given SNR
Symbol De-mapping using Log Map Demapper defined by "app".
- Generates Log likelihood values as hard_out is set to False.
De-rate matching
- Bit-Deselection
- Bit-Deinterleaving
LDPC Decoding
BER computation

The flow of the implementation can be understood using folowing diagram: LDPCCodes

The bit error rate (BER) is computed for every combination of code-rate \(= \{0.33, 0.4, 0.5, 0.67, 0.75, 0.83, 0.89\}\) and SNR \(= \{-5 , -2.5, 0 , 2.5, 5\}\) dB.

[5]:

tbSize     = 32
numBatches = 10

codeRate   = np.array([0.33, 0.5, 0.75, 0.89])
SNRdB      = np.linspace(-5,5,5)
SNR        = 10**(0.1*SNRdB)


BER        = np.zeros((codeRate.size, SNRdB.size))
rIndex     = 0
snrIndex   = 0

for coderate in codeRate:
    lpdcConfig = LDPCparameters(tbSize, coderate)
    k          = lpdcConfig.k_ldpc

    bg         = lpdcConfig.baseGraph
    zc         = lpdcConfig.liftingfactor
    numCBs     = lpdcConfig.numCodeBlocks
    N          = lpdcConfig.n

    bits       = np.float32(np.random.randint(2, size = (numBatches, numCBs, k), dtype=np.int8))
    encoder    = LDPCEncoder5G(k, bg, zc)
    encBits    = encoder(bits)
    E          = int(k/coderate)
    rateMatch  = BitSelection(numLayers=1, modOrder=2, numCodedBits=E, baseGraph=bg, enableLBRM=False, tbSize=tbSize, numCBs=numCBs)
    codeword   = rateMatch(encBits, rvID=0)
    symbols    = mapper(codeword[0])
    snrIndex   = 0
    for snr in SNR:

        symbs      = symbols + np.sqrt(0.5/snr)*(np.random.standard_normal(size=symbols.shape)+1j*np.random.standard_normal(size=symbols.shape)).astype(np.complex64)

        llrs       = demapper([symbs , np.float32(1/snr)])

        rxCodeword = BitDeselection(fillerIndices=np.array([]), baseGraph=bg,
                                    liftingFactor=zc, enableLBRM=False)([llrs], rvID=0)
        decoder    = LDPCDecoder5G(bg, zc)
        decBits    = decoder(rxCodeword)
        BER[rIndex, snrIndex] = np.mean(np.abs(decBits-bits))
        print("For coderate="+str(coderate)+" ("+str(k/codeword[0].shape[-1])+"), At SNR(dB): "+str(SNRdB[snrIndex])+" | Bit Error Rate: "+str(BER[rIndex, snrIndex]))
        snrIndex += 1
    rIndex   += 1

For coderate=0.33 (0.3305785123966942), At SNR(dB): -5.0 | Bit Error Rate: 0.2787500023841858
For coderate=0.33 (0.3305785123966942), At SNR(dB): -2.5 | Bit Error Rate: 0.25
For coderate=0.33 (0.3305785123966942), At SNR(dB): 0.0 | Bit Error Rate: 0.011250000447034836
For coderate=0.33 (0.3305785123966942), At SNR(dB): 2.5 | Bit Error Rate: 0.0
For coderate=0.33 (0.3305785123966942), At SNR(dB): 5.0 | Bit Error Rate: 0.0
For coderate=0.5 (0.5), At SNR(dB): -5.0 | Bit Error Rate: 0.32124999165534973
For coderate=0.5 (0.5), At SNR(dB): -2.5 | Bit Error Rate: 0.26625001430511475
For coderate=0.5 (0.5), At SNR(dB): 0.0 | Bit Error Rate: 0.16875000298023224
For coderate=0.5 (0.5), At SNR(dB): 2.5 | Bit Error Rate: 0.02250000089406967
For coderate=0.5 (0.5), At SNR(dB): 5.0 | Bit Error Rate: 0.0
For coderate=0.75 (0.7547169811320755), At SNR(dB): -5.0 | Bit Error Rate: 0.32749998569488525
For coderate=0.75 (0.7547169811320755), At SNR(dB): -2.5 | Bit Error Rate: 0.29249998927116394
For coderate=0.75 (0.7547169811320755), At SNR(dB): 0.0 | Bit Error Rate: 0.2175000011920929
For coderate=0.75 (0.7547169811320755), At SNR(dB): 2.5 | Bit Error Rate: 0.15625
For coderate=0.75 (0.7547169811320755), At SNR(dB): 5.0 | Bit Error Rate: 0.036249998956918716
For coderate=0.89 (0.8888888888888888), At SNR(dB): -5.0 | Bit Error Rate: 0.32249999046325684
For coderate=0.89 (0.8888888888888888), At SNR(dB): -2.5 | Bit Error Rate: 0.2874999940395355
For coderate=0.89 (0.8888888888888888), At SNR(dB): 0.0 | Bit Error Rate: 0.2537499964237213
For coderate=0.89 (0.8888888888888888), At SNR(dB): 2.5 | Bit Error Rate: 0.17624999582767487
For coderate=0.89 (0.8888888888888888), At SNR(dB): 5.0 | Bit Error Rate: 0.07874999940395355

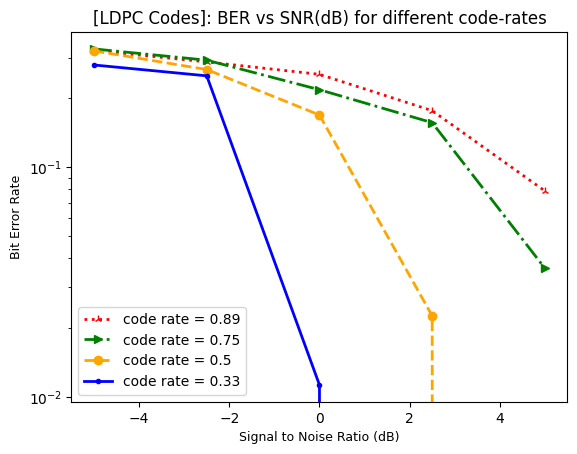
Performance Evaluation: BER vs SNR for different code-rates

The script plots SNR in dB vs BER performance at code-rate \(= \{0.33, 0.4, 0.5, 0.67, 0.75, 0.83, 0.89\}\). It can be observed that the Reed Muller codes can provide the reliablilty of

\(99.99990 \text{ or BER = } 10^{-4}\) for coderate \(\leq 0.5\) at an SNR value \(\leq 5\)dB.
For higher coderates higher SNR values are required to achieve the same performance.

Furthermore, the following averaged over \(500000\) batches (monteCarloIterations).

[6]:

fig, ax = plt.subplots()

color_tuple     = ['blue', 'orange', 'green',   'red',    'purple', 'brown',       'pink',  'gray', 'olive', 'cyan', 'black']
markcolor_tuple = ['gold', 'navy',   'crimson', 'yellow', 'line',   'springgreen', 'black', 'aqua', 'royalblue', 'red', 'green']
linestyle_tuple = ['-', '--', '-.', ':', 'solid', 'dashed', 'dashdot', 'dotted']
marker_tuple    = [".", "o", ">", "2", "8", "s", "p", "*", "P", "X", "D"]

rIndex = codeRate.size-1
for coderate in np.flip(codeRate):
    ax.semilogy(SNRdB, BER[rIndex], color=color_tuple[rIndex%len(color_tuple)],
                linestyle=linestyle_tuple[rIndex%len(linestyle_tuple)], lw = 2,
                marker=marker_tuple[rIndex%len(marker_tuple)], markersize = 6, label="code rate = "+str(coderate))

    rIndex = rIndex - 1

ax.legend(loc="lower left")
ax.set_xlabel("Signal to Noise Ratio (dB)", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("[LDPC Codes]: BER vs SNR(dB) for different code-rates", fontsize = 12)
plt.rcParams.update({'font.size': 9})
plt.show()

../../../_images/api_Tutorials_Tutorial4_Tutorial4_LDPCCodes_11_0.png

Simulation: Variation in Reliability with block-length for fixed coderate

[7]:

tbSize     = np.array([32, 128, 512, 2048, 8192])
numBatches = 100

codeRate   = np.array([0.5])
SNRdB      = np.linspace(-5,5,5)
SNR        = 10**(0.1*SNRdB)

BER        = np.zeros((tbSize.size, SNRdB.size))
rIndex     = 0
snrIndex   = 0
tbIndex    = 0

for tbsize in tbSize:
    rIndex     = 0
    for coderate in codeRate:
        lpdcConfig = LDPCparameters(tbsize, coderate)
        k          = lpdcConfig.k_ldpc

        bg         = lpdcConfig.baseGraph
        zc         = lpdcConfig.liftingfactor
        numCBs     = lpdcConfig.numCodeBlocks
        N          = lpdcConfig.n

        bits       = np.float32(np.random.randint(2, size = (numBatches, numCBs, k), dtype=np.int8))
        encoder    = LDPCEncoder5G(k, bg, zc)
        encBits    = encoder(bits)
        E          = int(k/coderate)
        rateMatch  = BitSelection(numLayers=1, modOrder=2, numCodedBits=E, baseGraph=bg, enableLBRM=False, tbSize=tbSize, numCBs=numCBs)
        codeword   = rateMatch(encBits, rvID=0)
        symbols    = mapper(codeword[0])
        snrIndex   = 0
        for snr in SNR:

            symbs      = symbols + np.sqrt(0.5/snr)*(np.random.standard_normal(size=symbols.shape)+1j*np.random.standard_normal(size=symbols.shape)).astype(np.complex64)

            llrs       = demapper([symbs , np.float32(1/snr)])

            rxCodeword = BitDeselection(fillerIndices=np.array([]), baseGraph=bg,
                                        liftingFactor=zc, enableLBRM=False)([llrs], rvID=0)
            decoder    = LDPCDecoder5G(bg, zc)
            decBits    = decoder(rxCodeword)
            BER[tbIndex, snrIndex] = np.mean(np.abs(decBits-bits))
            print("For tbsize="+str(tbsize)+" ("+str(k/codeword[0].shape[-1])+"), At SNR(dB): "+str(SNRdB[snrIndex])+" | Bit Error Rate: "+str(BER[tbIndex, snrIndex]))
            snrIndex += 1
        rIndex   += 1
    tbIndex   += 1

For tbsize=32 (0.5), At SNR(dB): -5.0 | Bit Error Rate: 0.31975001096725464
For tbsize=32 (0.5), At SNR(dB): -2.5 | Bit Error Rate: 0.2562499940395355
For tbsize=32 (0.5), At SNR(dB): 0.0 | Bit Error Rate: 0.15012499690055847
For tbsize=32 (0.5), At SNR(dB): 2.5 | Bit Error Rate: 0.0017500000540167093
For tbsize=32 (0.5), At SNR(dB): 5.0 | Bit Error Rate: 0.0
For tbsize=128 (0.5), At SNR(dB): -5.0 | Bit Error Rate: 0.32233333587646484
For tbsize=128 (0.5), At SNR(dB): -2.5 | Bit Error Rate: 0.2644583284854889
For tbsize=128 (0.5), At SNR(dB): 0.0 | Bit Error Rate: 0.15429165959358215
For tbsize=128 (0.5), At SNR(dB): 2.5 | Bit Error Rate: 0.0
For tbsize=128 (0.5), At SNR(dB): 5.0 | Bit Error Rate: 0.0
For tbsize=512 (0.5), At SNR(dB): -5.0 | Bit Error Rate: 0.3272361159324646
For tbsize=512 (0.5), At SNR(dB): -2.5 | Bit Error Rate: 0.2646944522857666
For tbsize=512 (0.5), At SNR(dB): 0.0 | Bit Error Rate: 0.16170834004878998
For tbsize=512 (0.5), At SNR(dB): 2.5 | Bit Error Rate: 0.0
For tbsize=512 (0.5), At SNR(dB): 5.0 | Bit Error Rate: 0.0
For tbsize=2048 (0.5), At SNR(dB): -5.0 | Bit Error Rate: 0.3237692415714264
For tbsize=2048 (0.5), At SNR(dB): -2.5 | Bit Error Rate: 0.2660336494445801
For tbsize=2048 (0.5), At SNR(dB): 0.0 | Bit Error Rate: 0.16290384531021118
For tbsize=2048 (0.5), At SNR(dB): 2.5 | Bit Error Rate: 0.0
For tbsize=2048 (0.5), At SNR(dB): 5.0 | Bit Error Rate: 0.0
For tbsize=8192 (0.5), At SNR(dB): -5.0 | Bit Error Rate: 0.30405065417289734
For tbsize=8192 (0.5), At SNR(dB): -2.5 | Bit Error Rate: 0.24077533185482025
For tbsize=8192 (0.5), At SNR(dB): 0.0 | Bit Error Rate: 0.1438588947057724
For tbsize=8192 (0.5), At SNR(dB): 2.5 | Bit Error Rate: 0.0
For tbsize=8192 (0.5), At SNR(dB): 5.0 | Bit Error Rate: 0.0

Performance Evaluation: BER vs SNR for different block lengths

[8]:

fig, ax = plt.subplots()

color_tuple     = ['blue', 'orange', 'green',   'red',    'purple', 'brown',       'pink',  'gray', 'olive', 'cyan', 'black']
markcolor_tuple = ['gold', 'navy',   'crimson', 'yellow', 'line',   'springgreen', 'black', 'aqua', 'royalblue', 'red', 'green']
linestyle_tuple = ['-', '--', '-.', ':', 'solid', 'dashed', 'dashdot', 'dotted']
marker_tuple    = [".", "o", ">", "2", "8", "s", "p", "*", "P", "X", "D"]

rIndex = 0
for tbsize in tbSize:
    ax.semilogy(SNRdB, BER[rIndex], color=color_tuple[rIndex%len(color_tuple)],
                linestyle=linestyle_tuple[rIndex%len(linestyle_tuple)], lw = 2,
                marker=marker_tuple[rIndex%len(marker_tuple)], markersize = 6, label="block-length = "+str(tbsize))

    rIndex = rIndex + 1

ax.legend(loc="lower left")
ax.set_xlabel("Signal to Noise Ratio (dB)", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("[LDPC Codes]: BER vs SNR(dB) for different block-length for fixxed code-rate = 0.5", fontsize = 12)
plt.rcParams.update({'font.size': 9})
plt.show()

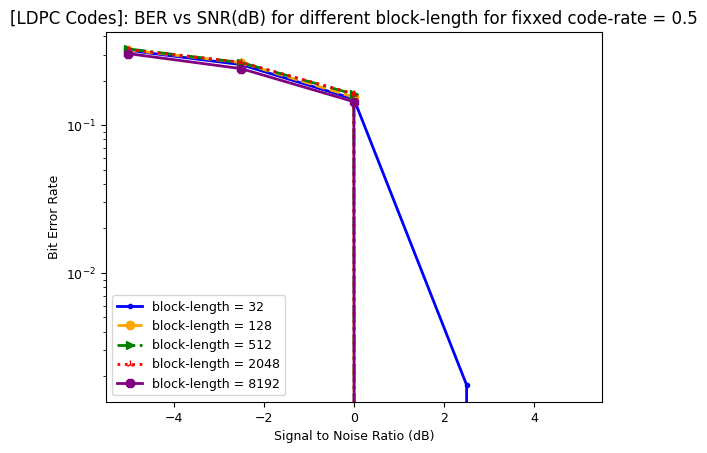
../../../_images/api_Tutorials_Tutorial4_Tutorial4_LDPCCodes_15_0.png

Following results are averaged over 100 results

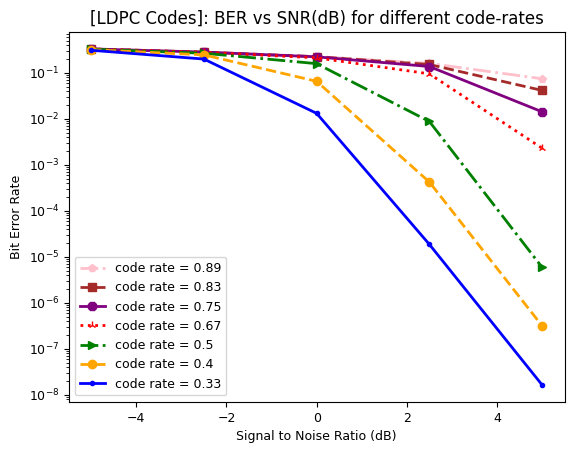
BER vs SNR

[9]:

ds       = np.load("Databases/BER_vs_SNR/LDPC_BERvsSNR_Final.npz")
BER      = ds["BER"]
SNRdB    = ds["SNRdB"]
codeRate = ds["codeRate"]

fig, ax = plt.subplots()

color_tuple     = ['blue', 'orange', 'green',   'red',    'purple', 'brown',       'pink',  'gray', 'olive', 'cyan', 'black']
markcolor_tuple = ['gold', 'navy',   'crimson', 'yellow', 'line',   'springgreen', 'black', 'aqua', 'royalblue', 'red', 'green']
linestyle_tuple = ['-', '--', '-.', ':', 'solid', 'dashed', 'dashdot', 'dotted']
marker_tuple    = [".", "o", ">", "2", "8", "s", "p", "*", "P", "X", "D"]

rIndex = codeRate.size-1
for coderate in np.flip(codeRate):
    ax.semilogy(SNRdB, BER[rIndex], color=color_tuple[rIndex%len(color_tuple)],
                linestyle=linestyle_tuple[rIndex%len(linestyle_tuple)], lw = 2,
                marker=marker_tuple[rIndex%len(marker_tuple)], markersize = 6, label="code rate = "+str(coderate))

    rIndex = rIndex - 1

ax.legend(loc="lower left")
ax.set_xlabel("Signal to Noise Ratio (dB)", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("[LDPC Codes]: BER vs SNR(dB) for different code-rates", fontsize = 12)
plt.rcParams.update({'font.size': 9})
plt.show()

../../../_images/api_Tutorials_Tutorial4_Tutorial4_LDPCCodes_18_0.png

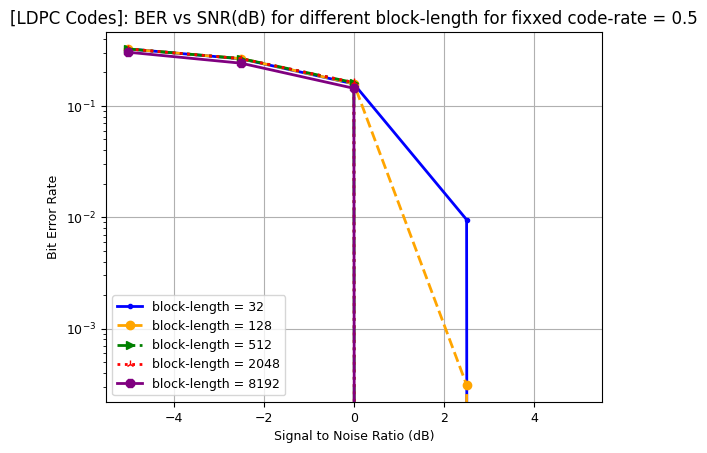
BER vs TB-size

[10]:

ds = np.load("Databases/BER_vs_tbSize/LDPC_BERvsSNR_tbSize"+str(0)+".npz")

BER = np.zeros(ds["BER"].shape)
for i in range(100):
    if(i in [1,2,3,4]):
        continue
    else:
        ds = np.load("Databases/BER_vs_tbSize/LDPC_BERvsSNR_tbSize"+str(i)+".npz")
        BER = BER + ds['BER']

BER    = BER/96
SNRdB  = ds["SNRdB"]
tbSize = ds["tbSize"]


fig, ax = plt.subplots()

color_tuple     = ['blue', 'orange', 'green',   'red',    'purple', 'brown',       'pink',  'gray', 'olive', 'cyan', 'black']
markcolor_tuple = ['gold', 'navy',   'crimson', 'yellow', 'line',   'springgreen', 'black', 'aqua', 'royalblue', 'red', 'green']
linestyle_tuple = ['-', '--', '-.', ':', 'solid', 'dashed', 'dashdot', 'dotted']
marker_tuple    = [".", "o", ">", "2", "8", "s", "p", "*", "P", "X", "D"]

rIndex = 0
for tbsize in tbSize:
    ax.semilogy(SNRdB, BER[rIndex], color=color_tuple[rIndex%len(color_tuple)],
                linestyle=linestyle_tuple[rIndex%len(linestyle_tuple)], lw = 2,
                marker=marker_tuple[rIndex%len(marker_tuple)], markersize = 6, label="block-length = "+str(tbsize))

    rIndex = rIndex + 1

ax.legend(loc="lower left")
ax.set_xlabel("Signal to Noise Ratio (dB)", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("[LDPC Codes]: BER vs SNR(dB) for different block-length for fixxed code-rate = 0.5", fontsize = 12)
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()

../../../_images/api_Tutorials_Tutorial4_Tutorial4_LDPCCodes_20_0.png

[ ]: