Reed Muller Codes in 5G
The Reed Muller codes are used in 5G to encode the small payload of control information having a block length between 3 to 11. These codes are linear block codes which generalizes the Reed–Solomon codes and the Walsh–Hadamard code. These codes are - locally testable, - locally decodable, and - list decodable.
In this tutorial, we will analyze the bit error rate performance of Reed Muller Codes for different link conditions characterized by signal to noise ratio(SNR). We further will demonstrate the variation in performance with block-length. The content of the tutorial is as follows:
Table of content:
Import Libraries
Python Libraries
[1]:
# %matplotlib widget
import matplotlib.pyplot as plt
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
import matplotlib as mpl
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes
from mpl_toolkits.axes_grid1.inset_locator import mark_inset
import numpy as np
5G Toolkit Libraries
[2]:
# import sys
# sys.path.append("../../../dist2/python3_11/")
import sys
sys.path.append("../../../")
from toolkit5G.SymbolMapping import Demapper
from toolkit5G.SymbolMapping import Mapper
from toolkit5G.ChannelCoder import ReedMullerEncoder5G
from toolkit5G.ChannelCoder import ReedMullerDecoder5G
[3]:
# from IPython.display import display, HTML
# display(HTML("<style>.container { width:100% !important; }</style>"))
Mapper and Demapper Parameters
Symbol mapping/Demapping is performed for:
BPSK constellation defined by
constellation_typewhich encodes1 bit per contellation symbol defined by
num_bits_per_symbol.The demapper generates log likelihood ratios configured by
hard_outusing a Log-Map (“app”) decoder defined using
demapping_method.
[4]:
constellation_type = "bpsk"
num_bits_per_symbol = 1
hard_out = False
demapping_method = "app"
mapper = Mapper(constellation_type, num_bits_per_symbol)
demapper= Demapper(demapping_method, constellation_type, num_bits_per_symbol, hard_out = hard_out)
Simulation Parameters
The simulations parameters are:
Kdefines block-length.SNRdBdefines Signal to noise ratio (SNR) in dB.numBatchesdefines number of batches to compute average BER.
[5]:
K = np.arange(1,12)
SNRdB = np.linspace(-10,0,5)
SNR = 10**(SNRdB/10)
numBatches = 5000
Simulation
This subsection performs the simulation which involve following steps:
Bits generation of length
kReed Muller Encoding
BPSK Symbol Mapping of encoded bits
Passing through the AWGN Channel
Adding noise to BPSK symbols with a given SNR
Symbol De-mapping using Log Map Demapper defined by
"app".Generates Log likelihood values as
hard_outis set toFalse.
Reed Muller Decoding
BER computation
The flow of the implementation can be understood using folowing diagram: 
The bit error rate (BER) is computed for every combination of K \(= \{1,2,3,\dots,11\}\) and SNR \(= \{-10, -8, -6, -4, -2, 0\}\) dB and averaged over \(500000\) batches (monteCarloIterations).
[6]:
BER = np.zeros((K.size, SNR.size))
kIndex = 0
snrIndex = 0
for k in K:
#######################################################
################ Generate UCI Payload #################
#######################################################
bits = np.random.randint(2, size = (numBatches, k))
#######################################################
################ Reed Muller Encoder ##################
#######################################################
codeword = ReedMullerEncoder5G()(bits)
#######################################################
################### Symbol Mapping ####################
#######################################################
symbols = mapper(codeword)
decoder = ReedMullerDecoder5G(k, hard_out)
snrIndex = 0
for snr in SNR:
#######################################################
################ Add Noise at Receiver ################
#######################################################
symbs = symbols + np.sqrt(0.5/snr)*(np.random.standard_normal(size=symbols.shape)+1j*np.random.standard_normal(size=symbols.shape)).astype(np.complex64)
#######################################################
################## Symbol Demapping ###################
#######################################################
llrEst = demapper([symbs, np.float32(1/snr)])
#######################################################
################ Reed Muller Decoder ##################
#######################################################
rxBits = decoder(llrEst)
#######################################################
############## Key Performance Metrics ################
#######################################################
BER[kIndex, snrIndex] = np.mean(np.abs(rxBits-bits))
print("For K="+str(k)+", At SNR(dB): "+str(SNRdB[snrIndex])+" | Bit Error Rate: "+str(BER[kIndex, snrIndex]))
snrIndex = snrIndex + 1
kIndex = kIndex + 1
For K=1, At SNR(dB): -10.0 | Bit Error Rate: 0.211
For K=1, At SNR(dB): -7.5 | Bit Error Rate: 0.0886
For K=1, At SNR(dB): -5.0 | Bit Error Rate: 0.012
For K=1, At SNR(dB): -2.5 | Bit Error Rate: 0.0002
For K=1, At SNR(dB): 0.0 | Bit Error Rate: 0.0
For K=2, At SNR(dB): -10.0 | Bit Error Rate: 0.2209
For K=2, At SNR(dB): -7.5 | Bit Error Rate: 0.087
For K=2, At SNR(dB): -5.0 | Bit Error Rate: 0.011
For K=2, At SNR(dB): -2.5 | Bit Error Rate: 0.0003
For K=2, At SNR(dB): 0.0 | Bit Error Rate: 0.0
For K=3, At SNR(dB): -10.0 | Bit Error Rate: 0.22253333333333333
For K=3, At SNR(dB): -7.5 | Bit Error Rate: 0.09186666666666667
For K=3, At SNR(dB): -5.0 | Bit Error Rate: 0.014066666666666667
For K=3, At SNR(dB): -2.5 | Bit Error Rate: 0.0003333333333333333
For K=3, At SNR(dB): 0.0 | Bit Error Rate: 0.0
For K=4, At SNR(dB): -10.0 | Bit Error Rate: 0.2183
For K=4, At SNR(dB): -7.5 | Bit Error Rate: 0.0982
For K=4, At SNR(dB): -5.0 | Bit Error Rate: 0.01245
For K=4, At SNR(dB): -2.5 | Bit Error Rate: 0.0003
For K=4, At SNR(dB): 0.0 | Bit Error Rate: 0.0
For K=5, At SNR(dB): -10.0 | Bit Error Rate: 0.21296
For K=5, At SNR(dB): -7.5 | Bit Error Rate: 0.0866
For K=5, At SNR(dB): -5.0 | Bit Error Rate: 0.01604
For K=5, At SNR(dB): -2.5 | Bit Error Rate: 0.00064
For K=5, At SNR(dB): 0.0 | Bit Error Rate: 0.0
For K=6, At SNR(dB): -10.0 | Bit Error Rate: 0.22046666666666667
For K=6, At SNR(dB): -7.5 | Bit Error Rate: 0.08643333333333333
For K=6, At SNR(dB): -5.0 | Bit Error Rate: 0.013
For K=6, At SNR(dB): -2.5 | Bit Error Rate: 0.0005333333333333334
For K=6, At SNR(dB): 0.0 | Bit Error Rate: 0.0
For K=7, At SNR(dB): -10.0 | Bit Error Rate: 0.422
For K=7, At SNR(dB): -7.5 | Bit Error Rate: 0.29897142857142855
For K=7, At SNR(dB): -5.0 | Bit Error Rate: 0.12937142857142858
For K=7, At SNR(dB): -2.5 | Bit Error Rate: 0.016457142857142858
For K=7, At SNR(dB): 0.0 | Bit Error Rate: 0.0
For K=8, At SNR(dB): -10.0 | Bit Error Rate: 0.419075
For K=8, At SNR(dB): -7.5 | Bit Error Rate: 0.31415
For K=8, At SNR(dB): -5.0 | Bit Error Rate: 0.13155
For K=8, At SNR(dB): -2.5 | Bit Error Rate: 0.017875
For K=8, At SNR(dB): 0.0 | Bit Error Rate: 0.00015
For K=9, At SNR(dB): -10.0 | Bit Error Rate: 0.41706666666666664
For K=9, At SNR(dB): -7.5 | Bit Error Rate: 0.3154888888888889
For K=9, At SNR(dB): -5.0 | Bit Error Rate: 0.13177777777777777
For K=9, At SNR(dB): -2.5 | Bit Error Rate: 0.014177777777777777
For K=9, At SNR(dB): 0.0 | Bit Error Rate: 0.0003111111111111111
For K=10, At SNR(dB): -10.0 | Bit Error Rate: 0.42402
For K=10, At SNR(dB): -7.5 | Bit Error Rate: 0.31048
For K=10, At SNR(dB): -5.0 | Bit Error Rate: 0.12976
For K=10, At SNR(dB): -2.5 | Bit Error Rate: 0.016
For K=10, At SNR(dB): 0.0 | Bit Error Rate: 0.00034
For K=11, At SNR(dB): -10.0 | Bit Error Rate: 0.42805454545454547
For K=11, At SNR(dB): -7.5 | Bit Error Rate: 0.31236363636363634
For K=11, At SNR(dB): -5.0 | Bit Error Rate: 0.1381090909090909
For K=11, At SNR(dB): -2.5 | Bit Error Rate: 0.0156
For K=11, At SNR(dB): 0.0 | Bit Error Rate: 0.0001818181818181818
Performance Evaluation
The script plots SNR in dB vs BER performance for block-length \(\in \{1,2,3,\dots,11\}\). It can be observed that the Reed Muller codes can provide the reliablilty of
\(99.99990 \text{ or BER = } 10^{-4}\) for block-length \(\in \{1,2,3,4,5\}\) and,
\(99.99999 \text{ or BER = } 10^{-5}\) for block-length \(\in \{1,2,3,\dots,11\}\) at an SNR value of 0 dB. Furthermore, the larger codeblock-lengths perform poorer compare to the small block-lengths.
[11]:
fig, ax = plt.subplots()
color_tuple = ['blue', 'orange', 'green', 'red', 'purple', 'brown', 'pink', 'gray', 'olive', 'cyan', 'black']
markcolor_tuple = ['gold', 'navy', 'crimson', 'yellow', 'line', 'springgreen', 'black', 'aqua', 'royalblue', 'red', 'green']
linestyle_tuple = ['-', '--', '-.', ':', 'solid', 'dashed', 'dashdot', 'dotted']
marker_tuple = [".", "o", ">", "2", "8", "s", "p", "*", "P", "X", "D"]
kIndex = 10
for k in np.flip(K):
ax.semilogy(SNRdB, BER[kIndex], color=color_tuple[kIndex%len(color_tuple)],
linestyle=linestyle_tuple[kIndex%len(linestyle_tuple)], lw = 3,
marker=marker_tuple[kIndex%len(marker_tuple)], markersize = 9, label="K = "+str(k))
kIndex = kIndex -1
ax.legend(loc="lower left")
ax.set_xlabel("Signal to Noise Ratio (dB)", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("[Reed Muller Codes]: SNR(dB) vs BER for various block-length")
plt.show()
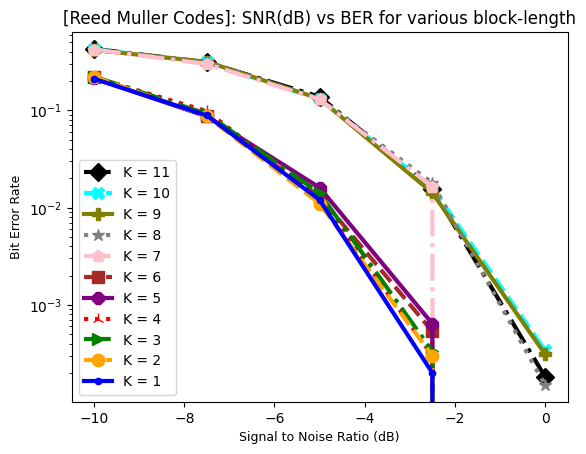
Performance Plot: Averaged over 65 datasets of 5000 points each.
[9]:
BERn = np.zeros((K.size, SNR.size))
for i in range(66):
ds = np.load("Database/BERvsSNR"+str(i)+".npz")
BERn = BERn + ds['BER']
BERn = BERn/66
fig, ax = plt.subplots()
color_tuple = ['blue', 'orange', 'green', 'red', 'purple', 'brown', 'pink', 'gray', 'olive', 'cyan', 'black']
markcolor_tuple = ['gold', 'navy', 'crimson', 'yellow', 'line', 'springgreen', 'black', 'aqua', 'royalblue', 'red', 'green']
linestyle_tuple = ['-', '--', '-.', ':', 'solid', 'dashed', 'dashdot', 'dotted']
marker_tuple = [".", "o", ">", "2", "8", "s", "p", "*", "P", "X", "D"]
# Make the zoom-in plot:
axins = zoomed_inset_axes(ax, 100, loc="upper right") # zoom = 100
axins2 = zoomed_inset_axes(ax, 100, loc="lower center") # zoom = 100
kIndex = 10
for k in np.flip(K):
ax.semilogy(SNRdB, BERn[kIndex], color=color_tuple[kIndex%len(color_tuple)],
linestyle=linestyle_tuple[kIndex%len(linestyle_tuple)], lw = 3,
marker=marker_tuple[kIndex%len(marker_tuple)], markersize = 9, label="K = "+str(k))
axins.semilogy(SNRdB, BERn[kIndex], color=color_tuple[kIndex%len(color_tuple)],
linestyle=linestyle_tuple[kIndex%len(linestyle_tuple)],
marker=marker_tuple[kIndex%len(marker_tuple)], markersize = 9, label="K = "+str(k))
axins2.semilogy(SNRdB, BERn[kIndex], color=color_tuple[kIndex%len(color_tuple)],
linestyle=linestyle_tuple[kIndex%len(linestyle_tuple)],
marker=marker_tuple[kIndex%len(marker_tuple)], markersize = 9, label="K = "+str(k))
kIndex = kIndex -1
ax.legend(loc="lower left")
ax.set_xlabel("Signal to Noise Ratio (dB)", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("[Reed Muller Codes]: SNR(dB) vs BER for various block-length")
#I want to select the x-range for the zoomed region. I have figured it out suitable values
# by trial and error. How can I pass more elegantly the dates as something like
# select y-range for zoomed region
x1 = -4.99
x2 = -5.01
# select y-range for zoomed region
y1 = 0.1295
y2 = 0.13375
axins.set_xlim(x1, x2)
axins.set_ylim(y1, y2)
plt.xticks(visible=False)
plt.yticks(visible=False)
mark_inset(ax, axins, loc1=2, loc2=3, fc="none", ec="0.5")
# select y-range for zoomed region
x1 = -4.99
x2 = -5.01
# select y-range for zoomed region
y1 = 0.0127
y2 = 0.01325
axins2.set_xlim(x1, x2)
axins2.set_ylim(y1, y2)
plt.xticks(visible=False)
plt.yticks(visible=False)
mark_inset(ax, axins2, loc1=1, loc2=2, fc="none", ec="0.5")
plt.draw()
plt.show()
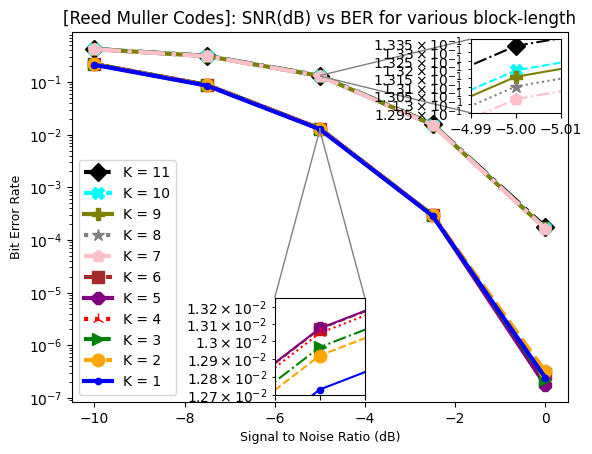
[ ]:
[ ]: