Hamming Codes

Hamming codes are perfect codes for (k,n) when \(k = 2^r-r-1\), \(n = 2^r-1\) where \(r\) is the number of parity bits. The code-rate (\(R = \frac{k}{n} = \frac{2^r-r-1}{2^r-1} = 1 - \frac{r}{2^r-1}\)) of Hamming codes increases as \(r\) increases. Hamming codes can detect \(1\) or \(2\) bit errors and can correct \(1\) bit error.

Table of Content:

Import Libraries
- Python Libraries
- 5G Toolkit Libraries
Hamming Codes Parameters
Simulation-Setup
Performance Evaluation: SNR vs BER
Performance Evaluation: SNR vs BLER
Conclusions

Import Libraries

Python Libraries

[1]:

import os
os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'

import numpy as np
# %matplotlib widget
import matplotlib.pyplot as plt

5G Toolkit Libraries

[2]:

# import sys
# sys.path.append("../../../dist2/python3_11/")

# import sys
# sys.path.append("../../../")
from toolkit5G.SymbolMapping import Demapper
from toolkit5G.SymbolMapping import Mapper
from toolkit5G.ChannelCoder  import HammingEncoder
from toolkit5G.ChannelCoder  import HammingDecoder

Hamming Codes Parameters

m is number of parity check bits
k is number of information bits
n is size of the codeword

[3]:

## Hamming Code Configurations
m = 3
k = 2**m - m - 1
n = 2**m - 1

Simulation Setup

numBatches defines numBatches.
bits information bits.
encBits encoded bits.
constellation_type constellation type.
num_bits_per_symbol number of bits per symbols.
demapping_method demapping methods.
hard_out if true symbol demapper return hard bits (0/1) otherwise log likelihood ratios are returned.

Note: For hard outputs, the syndrome based Hamming decoder is used. On the other hand for the soft outputs, the sphere decoder is used.

[4]:

## Payload Generation
numBatches = 100000
bits       = np.random.randint(2, size = (numBatches, k))

## Hamming Encoder
encBits = HammingEncoder(k,n)(bits)

## Rate Matching (No rate matching as of now)
codeword = encBits

## Symbol Mapping
constellation_type  = "bpsk"
num_bits_per_symbol = 1
mapperObject        = Mapper(constellation_type, num_bits_per_symbol)
symbols             = mapperObject(codeword)

SNRdB = np.linspace(-4,8,10)
SNR   = 10**(SNRdB/10)

uncodedBER    = np.zeros(SNR.shape)
codedBERhard  = np.zeros(SNR.shape)
codedBERsoft  = np.zeros(SNR.shape)
codedBLERhard = np.zeros(SNR.shape)
codedBLERsoft = np.zeros(SNR.shape)

## Symbol Demapping
demapping_method = "app"
hard_out         = False

demapper         = Demapper(demapping_method, constellation_type,
                            num_bits_per_symbol, hard_out = hard_out)
snrIndex = 0
for snr in SNR:

    # AWGN Channel
    symbs   = symbols + np.sqrt(0.5/snr)*(np.random.standard_normal(size=symbols.shape)+1j*np.random.standard_normal(size=symbols.shape)).astype(np.complex64)

    # Symbol Demapping
    llrEst  = demapper([symbs, np.float32(1/snr)])

    # Decoding based on Hard Inputs
    uncBits = np.where(llrEst > 0, np.int8(1), np.int8(0))
    uncodedBER[snrIndex] = np.mean(np.abs(uncBits-encBits))
    decoder = HammingDecoder(k,n)
    decBits = decoder(uncBits)

    # BER and BLER for decoding based on Hard Inputs
    codedBERhard[snrIndex] = np.mean(np.abs(bits-decBits))
    codedBLERhard[snrIndex]= np.mean(np.where(np.sum(np.abs(bits-decBits), axis=1)>0, True, False))

    # Decoding based on Soft Inputs
    decoder = HammingDecoder(k,n)
    decBits = decoder(llrEst, "sphereDecoding")

    # BER and BLER for decoding based on Soft Inputs
    codedBERsoft[snrIndex] = np.mean(np.abs(bits-decBits))
    codedBLERsoft[snrIndex]= np.mean(np.where(np.sum(np.abs(bits-decBits), axis=1)>0, True, False))

    print("At SNR(dB): "+str(SNRdB[snrIndex])+" | coded BER: "+str(codedBERhard[snrIndex])+" | uncoded BER: "+str(uncodedBER[snrIndex]))

    snrIndex += 1

At SNR(dB): -4.0 | coded BER: 0.17671 | uncoded BER: 0.18611285714285714
At SNR(dB): -2.666666666666667 | coded BER: 0.12653 | uncoded BER: 0.14775285714285713
At SNR(dB): -1.3333333333333335 | coded BER: 0.081805 | uncoded BER: 0.11270857142857142
At SNR(dB): 0.0 | coded BER: 0.0436425 | uncoded BER: 0.07803428571428571
At SNR(dB): 1.333333333333333 | coded BER: 0.0185 | uncoded BER: 0.04909714285714286
At SNR(dB): 2.666666666666666 | coded BER: 0.0063725 | uncoded BER: 0.027304285714285715
At SNR(dB): 4.0 | coded BER: 0.0014125 | uncoded BER: 0.01259
At SNR(dB): 5.333333333333332 | coded BER: 0.000145 | uncoded BER: 0.004475714285714286
At SNR(dB): 6.666666666666666 | coded BER: 5e-06 | uncoded BER: 0.0011442857142857142
At SNR(dB): 8.0 | coded BER: 0.0 | uncoded BER: 0.00018

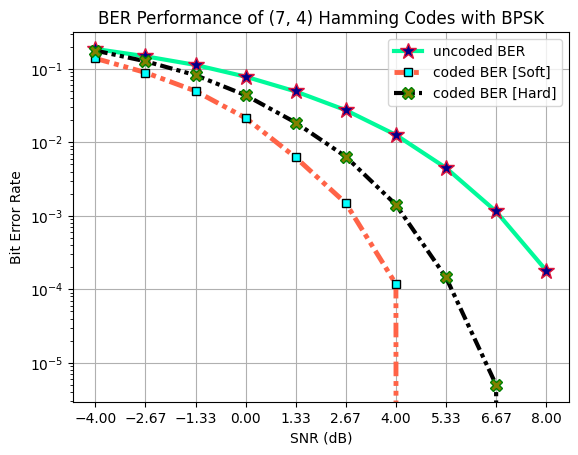
Performance Evaluation: SNR vs BER

Following plots demonstate the BER vs SNR performance of following:

Uncoded transmission (Hamming Code is not used)
Hamming decoder (Syndrome based decoder) taking hard bits (0/1) as inputs.
Hamming decoder (Sphere decoder) taking soft bits (log likelihood ratios) as inputs.

[5]:

fig, ax = plt.subplots()

ax.semilogy(SNRdB, uncodedBER,   'mediumspringgreen', lw = 3, linestyle = "solid",
            marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "uncoded BER")
ax.semilogy(SNRdB, codedBERsoft, 'tomato', lw = 3.5, linestyle = (0, (3, 1, 1, 1, 1, 1)),
            marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "coded BER [Soft]")
ax.semilogy(SNRdB, codedBERhard, 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)),
            marker = "X", ms = 9, mec = "green", mfc = "olive", label = "coded BER [Hard]")
ax.legend()
ax.set_xticks(SNRdB)
ax.grid()
ax.set_ylabel("Bit Error Rate")
ax.set_xlabel("SNR (dB)")
ax.set_title("BER Performance of ("+str(n)+", "+str(k)+") Hamming Codes with BPSK")
plt.show()

../../../_images/api_Tutorials_Tutorial1_BER_Analysis_of_Hamming_Codes_10_0.png

Performance Evaluation: SNR vs BLER

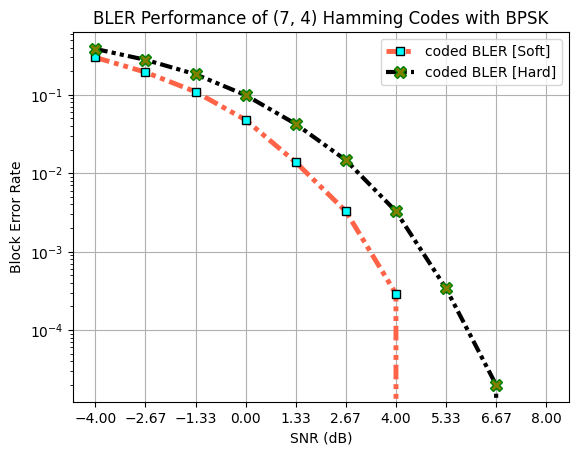
Following plots demonstate the BLER vs SNR performance of following:

Hamming decoder (Syndrome based decoder) taking hard bits (0/1) as inputs.
Hamming decoder (Sphere decoder) taking soft bits (log likelihood ratios) as inputs.

[6]:

fig, ax = plt.subplots()

ax.semilogy(SNRdB, codedBLERsoft, 'tomato', lw = 3.5, linestyle = (0, (3, 1, 1, 1, 1, 1)),
            marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "coded BLER [Soft]")
ax.semilogy(SNRdB, codedBLERhard, 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X",
            ms = 9, mec = "green", mfc = "olive", label = "coded BLER [Hard]")
ax.legend()
ax.set_xticks(SNRdB)
ax.grid()
ax.set_ylabel("Block Error Rate")
ax.set_xlabel("SNR (dB)")
ax.set_title("BLER Performance of ("+str(n)+", "+str(k)+") Hamming Codes with BPSK")
plt.show()

../../../_images/api_Tutorials_Tutorial1_BER_Analysis_of_Hamming_Codes_12_0.png

Conclusions

The Hamming decoder with soft inputs outputs the rest of the techniques for both BER as well as BLER.
Sphere Decoding has very high complexity which scales exponentially with parity bits (m).