Position Estimation

This package is used for estimating the location of a device using 5G Networks. 5G has standardized the positioning reference signal (PRS), methods and procedures to localize a node in either uplink or downlink based on power, angle or time/delay measurements as illustrated in table-1.

Table 36 Positioning in 5G Networks

Method	Measurements	positioningMethod	optimizationMethod
DL-TDoA	TDOA	TDOA	NewtonRaphson, GradientDescent
UL-TDoA	TDOA	TDOA, Hybrid TDoA + AoA	NewtonRaphson, GradientDescent
DL-AoD	RSRP, AoD	DOA	NewtonRaphson, GradientDescent
UL-AoA	RSRP, AoD, RToA	DOA, Hybrid TDoA + AoA	NewtonRaphson, GradientDescent
m-RTT	RSRP, RToA	TOA, Hybrid ToA + AoA	LeastSquare
ECID	RSRP	Not supported	Not supported

---

Position Estimation

Code example: Position Estimation using Time of Arrival (ToA/mRTT) Estimates

posEstimator = PositionEstimation(optimizationMethod = "LeastSquare")
# Position Estimation Object:
    # Positioning based on: ToA
    # Optimization Method: Least Square
    # txPosition: (numTranmitter, 3)
    # ToAe: (numTranmitter, )

posEstimate = posEstimator(refPosition=txPosition, toa=ToAe)

    # posEstimate will have a shape (2, 3)
    # Optimization Error can be accessed using posEstimate.error

posEstimator.display()

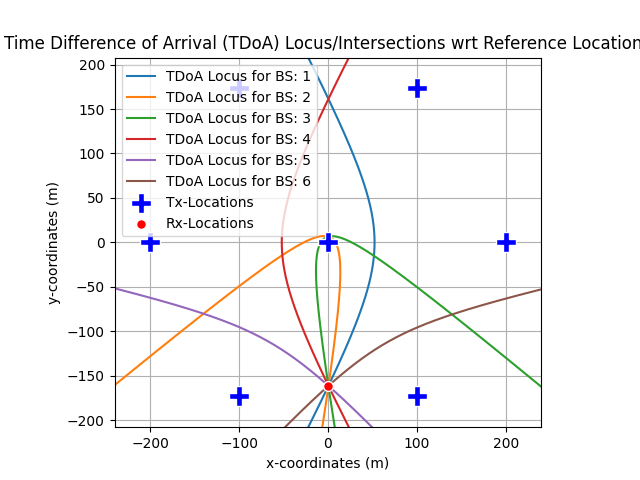
Code example: Position Estimation using Time Difference of Arrival (TDoA) Estimates

numIterations = 10000
numEpochs     = 10
tolerance     = 0.00000001
stepsize      = 0.1
isd           = 100
posEstimator  = PositionEstimation(optimizationMethod = "NewtonRaphson",
                                   numIterationPerEpoch = numIterations, numEpochs = numEpochs,
                                   tolerance = tolerance, stepsize = stepsize, isd = isd)
# Position Estimation Object:
    # Positioning based on: TDOA
    # Optimization Method: NewtonRaphson
    # txPosition: (numTranmitter, 3)
    # tdoaEst: (numTranmitter-1,)

posEstimate   = posEstimator(refPosition=txPosition, tdoa = tdoaEst)

posEstimator.display()

---

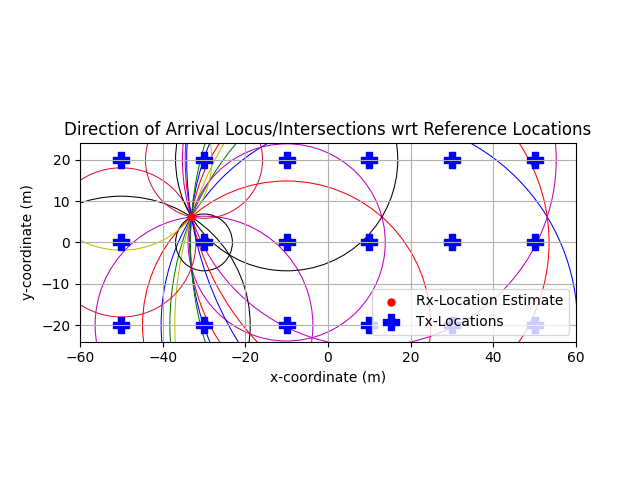
Code example: Position Estimation using Direction of Arrival (DoA) Estimates

numIterations = 10000
numEpochs     = 10
tolerance     = 0.00000001
stepsize      = 0.1
isd           = 100
posEstimator  = PositionEstimation(optimizationMethod = "GradientDescent",
                                   numIterationPerEpoch = numIterations, numEpochs = numEpochs,
                                   tolerance = tolerance, stepsize = stepsize, isd = isd)
# Position Estimation Object:
    # Positioning based on: DOA
    # Optimization Method: Gradient Descent
    # txPosition: (numTranmitter, 3)
    # doaEst: (numTranmitter, 2)

posEstimate   = posEstimator(refPosition=txPosition, xoA = doaEst)

posEstimator.display()

---

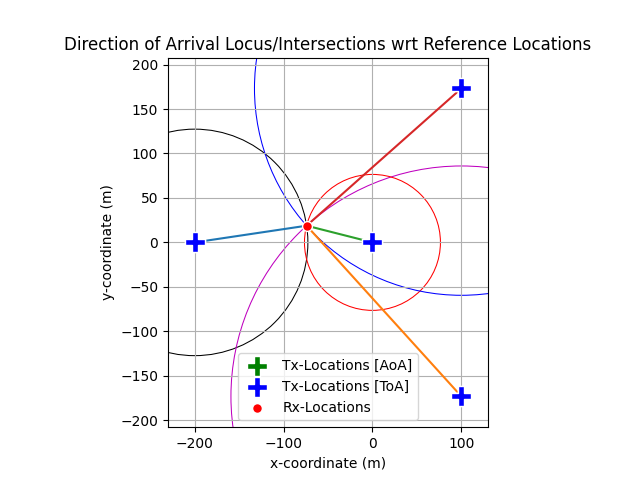
Code example: Position Estimation using Hybrid ToA/mRTT and Direction of Arrival (DoA) Estimates

posEstimator  = PositionEstimation(optimizationMethod = "LeastSquare")
# Position Estimation Object:
    # Positioning based on: Hybrid ToA + DOA
    # Optimization Method: Least Square
    # txPosition: (numTranmitter, 3)
    # doaEst: (numTranmitter, 2)
    # toaEst: (numTranmitter,)

posEstimate   = posEstimator(refPosition=txPositionToA, tdoa = toaEst, xoA = XoA)

posEstimator.display()

---

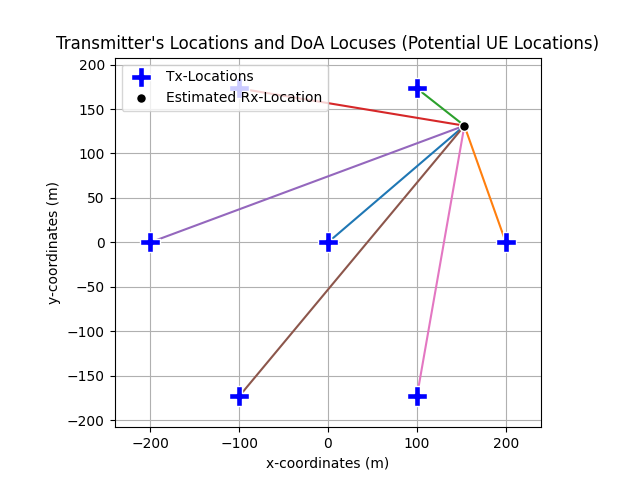
Code example: Position Estimation using Hybrid TDoA and Direction of Arrival (DoA) Estimates

posEstimator  = PositionEstimation(optimizationMethod = "LeastSquare")
# Position Estimation Object:
    # Positioning based on: Hybrid TDoA + DOA
    # Optimization Method: Least Square
    # txPosition: (numTranmitter, 3)
    # doaEst: (numTranmitter, 2)
    # tdoaEst: (numTranmitter-1,)

posEstimate   = posEstimator(refPosition=txPositionToA, tdoa = tdoaEst, xoA = XoA, refPositionAoA=txPositionAoA)

posEstimator.display()

---

API Documentation

The following section provides the details about the input and output interface for Position Estimator.

class toolkit5G.Positioning.PositionEstimation(optimizationMethod='LeastSquare', numIterationPerEpoch=10000, numEpochs=10, tolerance=1e-06, stepsize=0.1, isd=100)

This module provides a high level API to estimate the location of node/device based on the delay or time of arrival (ToA), time difference of arrival (TDoA) estimates.

Important

The numIterationPerEpoch, numEpochs, tolerance, stepsize, and isd parameters are relevant only for iterative optimizationMethod such as GradientDescent and NewtonRaphson. These parameters are ignored when optimizationMethod is LeastSquare.

Parameters:

• optimizationMethod (str) – Defines the method used for estimating the location of a node \(\in \{\)“LeastSquare”, “NewtonRaphson”, “GradientDescent” \(\}\). The default value is “LeastSquare”.

• numIterationPerEpoch (int) – Number of iteration for gradient descent optimizations for every epoch. Default value is 10000. .

• numEpochs (int) – Number of epoches used in gradient descent optimizations. In every epoch, the initial position estimate is chosen randomly. It help in avoiding the local minimas. Default value is 10.

• tolerance (float) – Error tolerance values. The optimization stops when the optimization error reduces below tolerance value.

• stepsize (float) – Optimization step size. The Newton Raphson algorithms iterates using this step-size to converge towards the global/local optimal solutions.

• isd (float) – Defines the intersite distance (in meter). Its equal to \(2 \times\) cell-radius.

Input:

• refPosition ((\(\text{N}_\text{ref}\),3), np.float) – Defines the location (in meters) of the reference nodes used for positioning where \(\text{N}_\text{ref}\) defines the number of reference nodes used for positioning.

• toa ((\(\text{N}_\text{ref}\),), np.float) – Defines the time of arrival measurements (in seconds) wrt every reference node used for positioning where \(\text{N}_\text{ref}\) defines the number of reference nodes.

• tdoa ((\(\text{N}_\text{ref}\)-1,), np.float) – Defines the time difference of arrival measurements (in seconds) wrt every reference node used for positioning where \(\text{N}_\text{ref}\) defines the number of reference nodes. For TDoA calculation the ToA measurement of the first node is considered as the basis for calculating the time difference.

• xoA ((\(\text{N}_\text{ref}\),2), np.float) – Defines the direction of arrival measurements (in radians) used for positioning where \(\text{N}_\text{ref}\) defines the number of reference nodes. The xoA[0] and xoA[1] denotes the azimuth and elevation angles of arrival w.r.t to every reference node.

Important

The optimizationMethod used for positioning estimation depends on the measurements input while calling object.

• If toa alone is passed, then ToA/mRTT based Positioning. For this, optimizationMethod can only be LeastSquare.

• If tdoa alone is passed, then TDoA based Positioning. For this, optimizationMethod can take one value from GradientDescent, NewtonRaphson or LeastSquare.

• If xoA alone is passed, then direction of arrival based Positioning. For this, optimizationMethod can either be GradientDescent or LeastSquare.

• If toa and xoA is passed, then ToA/mRTT + DoA based Hybrid Positioning. For this, optimizationMethod can only be LeastSquare.

• If tdoa and xoA alone is passed, then TDoA + DoA based Hybrid Positioning. For this, optimizationMethod can only be LeastSquare.

Output:

[k,3], np.float – returns the position Estimate. The value of k is 2 for the Least square estimator. The Least square estimator returns 2 position estimates, one above the reference locations and other below due to GDoP when the height of the ref nodes is same. For the remaining methods k is 1.

Attributes:

• error (np.float) – return the uncertainty in the position estimates.

• positionEstimator (positioning estimator object from OptimizationMethods)

Note

For ToA and AoA methods, the number of measurements must match the number of reference locations. On the other hand, for TDoA method, the number of measurements should be equal to \(\text{N}_\text{ref}-1\) and first location in refPosition should indicate the location of the node whose ToA measurement is taken as reference for computing TDoAs. The time difference of arrival is computed as \(\{ \Delta \tau_{i,r} = \tau_i - \tau_r\}_{i=0}^{i=\text{N}_\text{ref}-1} s.t. i \neq r\) where \(r\) is the reference measurement used for difference in TDoA. The location of node-r must be the at the first place in refPosition followed by the locations of the remaining nodes from the set \(\zeta = \{i | i \neq r\}_{i=0}^{i=\text{N}_\text{ref}-1}\).

• refPosition[:,0] = location of node-r

• refPosition[:,i] = location of node-\(\zeta[i]\)

Note

The large value of numIterationPerEpoch improves the optimization performance but increases the complexity of the method.

Note

The large value of numEpochs helps reduce the odds of getting stuck in the local optima but increases the complexity of the method.

Note

The lower value of tolerance improves the optimization performance but increases the complexity of the method. The method iterative longer to reduces the optimization error below the tolerance limit.

Note

The selection of step-size mu plays crucial role in performance of the method. Small step-size results in good performance but requires large number of iteration numIterationPerEpoch to converge. Large step-size improves the convergence rate but are suceptible to local minimas.

Raises:

• ValueError – “[Error]: ‘refPosition’ must be a numpy array!”

• ValueError – “[Error]: ‘refPosition’ must be an numpy array of size (numRefnode x 3)!”

• ValueError – “[Error]: ‘xoA’ must be a numpy array!”

• ValueError – “[Error]: shape of ‘xoA’ must be equal to (refPosition.shape[0],2)!”

• Warning – “[Warning-PositionEstimation]: Currently only ‘GradientDescent’ and ‘LeastSquare’ methods are supported! Defaulting to ‘LeastSquare’!”

• Warning – “[Warning-PositionEstimation]: Currently not supported! Defaulting to ‘GradientDescent’”

• Warning – “[Warning-PositionEstimation]: Currently only ‘NewtonRaphson’, ‘GradientDescent’, and ‘LeastSquare’ methods are supported! Defaulting to ‘LeastSquare’!”

• Warning – “[Warning-PositionEstimation]: Currently only ‘LeastSquare’ based optimization estimation is supported! Defaulting to ‘LeastSquare’!”

• Warning – “[Warning-PositionEstimation]: Currently only ‘LeastSquare’ based optimization estimation is supported! Defaulting to ‘LeastSquare’!”

• ValueError – “[Error]: ‘toa’ must be a numpy array!”

• ValueError – “[Error]: size of ‘toa’ must be equal to ‘num of reference nodes’(refPosition.shape[0])!”

• Warning – “[Warning-PositionEstimation]: Currently only ‘LeastSquare’ based optimization estimation is supported! Defaulting to ‘LeastSquare’!”

• Warning – “[Warning-PositionEstimation]: ‘ToA’ and ‘TDoA’ both are passed. No method to support hybrid positioning for this. Ignoring ‘TDoA’, defaulting to ToA based Positioning!”

• Warning – “[Warning-PositionEstimation]: Currently only ‘LeastSquare’ based optimization estimation is supported! Defaulting to ‘LeastSquare’!”

• ValueError – “[Error]: ‘toa’ must be a numpy array!”

• ValueError – “[Error]: size of ‘toa’ must be equal to ‘num of reference nodes’(refPosition.shape[0])!”

• ValueError – “[Error-PositionEstimation]: ‘positioningMethod’ must be one of ‘TOA’, ‘TDOA’, ‘DOA’!”

• ValueError – “[Error-PositionEstimation]: method must be ‘ESPRIT’, ‘MUSIC’, ‘PDP’!”

• ValueError – “[Error-PositionEstimation]: fig_ax_tuple must be a tuple!”

• ValueError – “[Error-PositionEstimation]: fig_ax_tuple[0] must be a ‘plt.Figure’ type object!”

• ValueError – “[Error-PositionEstimation]: fig_ax_tuple[1] must be a ‘plt.Axes’ type object!”

• Warning – “[Warning-PositionEstimation]: Currently visualization supported only for ‘TOA’ method!”

PositionEstimation.display(circlelw=0.75, circlels='-', estLocSize=100, estLocMarker='.', estLocColor='r', refLocSize=125, refLocMarker='P', refLocColor='b', fig_ax_tuple=None, displayLegends=True, displayPlot=True)

Display the locus of the time of arrival circles to check the optimization performance of the position estimation method.

Parameters:

• circlelw (float) – Defines the line-width of the plotted ToA locus circle. Default value is 0.4.

• circlels (str) – Defines the line-style of the plotted ToA locus circle. Default value is “–“.

• estLocSize (float) – Defines the size of the marker of the estimated node location. Default value is 100.

• estLocMarker (str) – Defines the type of the marker of the estimated node location. Default value is “.” (dot sign).

• estLocColor (str) – Defines the color of the marker of the estimated node location. Default value is “r” (red color).

• refLocSize (float) – Defines the size of the marker of the reference node location. Default value is 100..

• refLocMarker (str) – Defines the type of the marker of the reference node location. Default value is “P” (Plus sign).

• refLocColor (str) – Defines the color of the marker of the reference node location. Default value is “b” (blue color).

• fig_ax_tuple ((2,), tuple) –

  tuple containing 2 values. If passed, the plot will be appended to the inputted (fig, ax) object.

  • fig_ax_tuple[0] is the plt.Figure type object and,

  • fig_ax_tuple[1] is the plt.Axes type object.

• displayLegends (bool) – Flag allows to user to enable/disable the visibility of the new legends to the (fig, ax) object.

• displayPlot (bool) – Flag allows to user to decide wheather to display the plot or not. This flag is important when superimposing multiple plots and display them at once.

---

Submodules

• Time of Arrival (ToA)/Delay Estimation
  • ToAEstimation
  • DFT based Method
    • DFT_ToA
  • ESPRIT based ToA Estimation
    • ESPRIT_ToA
  • MUSIC based ToA Estimation
    • MUSIC_ToA
• Direction of Arrival Estimation
  • DoAEstimation
  • DFT based AoA Method
    • DFT_DoA
  • ESPRIT based DoA Estimation
    • ESPRIT_DoA
  • MUSIC based DoA Estimation
    • MUSIC_DoA
• Optimization Algorithms
  • Least Squares based Position Estimator for TDoA
    • LeastSquareTDoA
  • Gradient Descent based Position Estimator for TDoA
    • GradientDescentTDoA
  • Newton Raphson based Position Estimator for TDoA
    • NewtonRaphsonTDoA
  • Least Squares based Position Estimator for ToA/mRTT
    • LeastSquareToA
  • Least Squares based Position Estimator for DoA
    • LeastSquareDoA
  • Gradient Descent based Position Estimator for DoA
    • GradientDescentDoA
  • Least Square based Position Estimator for Hybrid ToA/mRTT and DoA
    • HybridToAAoA
  • Least Square based Position Estimator for Hybrid TDoA and DoA
    • HybridTDoAAoA