Selection of minimum CORESET Size for a Given Target Block Probability

In this notebook, we simulate a design problem in determining the minimum CORESET size needed for meeting a target blocking probability.
Specifically, given the number of UEs and the coverage condition, BS can properly determine the CORESET size to ensure the blocking probability does not exceed a specified threshold.
For evaluation, we consider the medium coverage condidtion where most of the UEs require medium ALs (i.e., AL 4), with AL distribution [0.05, 0.2, 0.5, 0.2, 0.05]
The CORESET size must increase when more UEs are scheduled and a smaller blocking probability target.
While a larger CORESET is beneficial for UE scheduling, it may not be desired from spectral and energy efficiency perspective, as more bandwith and more number of CCEs that a UE has to blindly look for. Therfore the network should properly select the CORESET size based on the requirements. So there is a trade off between CORESET size and target blocking probability.

Python Libraries

[1]:

import os
os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'

# %matplotlib widget
import matplotlib.pyplot  as plt
import matplotlib.patches as mpatches
import matplotlib as mpl

import numpy      as np

5G-Toolkit Libraries

[2]:

import sys
sys.path.append("../../")
from toolkit5G.Scheduler import PDCCHScheduler

Simulation Parameters

The following parameters are used for this simulation: - coresetID denotes the coreset ID. - slotNumber denotes the slot-number carrying the PDCCH. - searchSpaceType denotes the search space type. UE specific search space (USS) or Common search space (CSS). - nci denotes the variable corresponding to carrier aggregation. Current simulation does not assume carrier aggregation.

[3]:

mu                = np.random.randint(4)    # numerlogy for sub-carrier spacing
numSlotsPerFrame  = 2**mu * 10              # number of slots per radio frame
coresetID         = 1                       # coreset ID
slotNumber        = 0
searchSpaceType   = "USS"                   # search space type. UE specific search space
nci               = 0                       # variable corresponding to carrier aggregation
numIterations     = 1000

PDCCH Scheduling Parameters

Following parameters are crucial for PDCCH scheduling performance: - coresetSize denotes coreset size or number of CCEs available for scheduling UEs. - strategy denotes the scheduling strategy. - numCandidates denotes number of PDCCH candidates per each Aggregation Level (AL). - aggLevelProbDistribution denotes the probability distribution with which an AL is choosen for a UE by the scheduler.

[4]:

aggLevelProbDistribution = np.array([0.05, 0.2, 0.5, 0.2, 0.05])
minCCEs                  = 20
maxCCEs                  = 135
coresetSize              = np.arange(minCCEs,maxCCEs+1,5)
numCandidates            = np.array([135,67,33,16,8], dtype=int)
strategy                 = "Conservative"

pdcchSchedulerObj = PDCCHScheduler(mu, slotNumber, coresetID, nci)

Compute minimum coreset size for `numUEs` = 5.

[5]:

################
# For 5 UEs
################

numUEs         = 5
rnti           = np.random.choice( np.arange(1,65519+1), size = (numUEs,), replace=False)

probOfBlocking = np.zeros((coresetSize.size,))
for n in range(coresetSize.size):
    print("Simulating (n,numCCEs) : "+str(n)+", "+str(coresetSize[n]))
    Nccep     = coresetSize[n]
    prob      = 0
    for i in range(numIterations):
        ueALdistribution  = np.random.multinomial(numUEs, aggLevelProbDistribution)
        count             = pdcchSchedulerObj(Nccep,searchSpaceType,ueALdistribution,numCandidates,rnti,strategy)[0]
        numBlockedUEs     = np.sum(count)
        prob              = prob + (numBlockedUEs/numUEs)
    probOfBlocking[n] = prob/numIterations

targetBlockingProbability = 0.05
minCoresetSize5ForNumUEs5 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

targetBlockingProbability  = 0.10
minCoresetSize10ForNumUEs5 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

targetBlockingProbability  = 0.15
minCoresetSize15ForNumUEs5 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

targetBlockingProbability  = 0.20
minCoresetSize20ForNumUEs5 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

Simulating (n,numCCEs) : 0, 20
Simulating (n,numCCEs) : 1, 25
Simulating (n,numCCEs) : 2, 30
Simulating (n,numCCEs) : 3, 35
Simulating (n,numCCEs) : 4, 40
Simulating (n,numCCEs) : 5, 45
Simulating (n,numCCEs) : 6, 50
Simulating (n,numCCEs) : 7, 55
Simulating (n,numCCEs) : 8, 60
Simulating (n,numCCEs) : 9, 65
Simulating (n,numCCEs) : 10, 70
Simulating (n,numCCEs) : 11, 75
Simulating (n,numCCEs) : 12, 80
Simulating (n,numCCEs) : 13, 85
Simulating (n,numCCEs) : 14, 90
Simulating (n,numCCEs) : 15, 95
Simulating (n,numCCEs) : 16, 100
Simulating (n,numCCEs) : 17, 105
Simulating (n,numCCEs) : 18, 110
Simulating (n,numCCEs) : 19, 115
Simulating (n,numCCEs) : 20, 120
Simulating (n,numCCEs) : 21, 125
Simulating (n,numCCEs) : 22, 130
Simulating (n,numCCEs) : 23, 135

Compute minimum coreset size for `numUEs` = 10.

[6]:

################
# For 10 UEs
################

numUEs         = 10
rnti           = np.random.choice( np.arange(1,65519+1), size = (numUEs,), replace=False)

probOfBlocking = np.zeros((coresetSize.size,))
for n in range(coresetSize.shape[0]):
    print("Simulating (n,numCCEs) : "+str(n)+", "+str(coresetSize[n]))
    Nccep     = coresetSize[n]
    prob      = 0
    for i in range(numIterations):
        ueALdistribution  = np.random.multinomial(numUEs, aggLevelProbDistribution)
        count             = pdcchSchedulerObj(Nccep,searchSpaceType,ueALdistribution,numCandidates,rnti,strategy)[0]
        numBlockedUEs     = np.sum(count)
        prob              = prob + (numBlockedUEs/numUEs)
    probOfBlocking[n] = prob/numIterations

targetBlockingProbability   = 0.05
minCoresetSize5ForNumUEs10  = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

targetBlockingProbability   = 0.10
minCoresetSize10ForNumUEs10 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

targetBlockingProbability   = 0.15
minCoresetSize15ForNumUEs10 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

targetBlockingProbability   = 0.20
minCoresetSize20ForNumUEs10 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

Simulating (n,numCCEs) : 0, 20
Simulating (n,numCCEs) : 1, 25
Simulating (n,numCCEs) : 2, 30
Simulating (n,numCCEs) : 3, 35
Simulating (n,numCCEs) : 4, 40
Simulating (n,numCCEs) : 5, 45
Simulating (n,numCCEs) : 6, 50
Simulating (n,numCCEs) : 7, 55
Simulating (n,numCCEs) : 8, 60
Simulating (n,numCCEs) : 9, 65
Simulating (n,numCCEs) : 10, 70
Simulating (n,numCCEs) : 11, 75
Simulating (n,numCCEs) : 12, 80
Simulating (n,numCCEs) : 13, 85
Simulating (n,numCCEs) : 14, 90
Simulating (n,numCCEs) : 15, 95
Simulating (n,numCCEs) : 16, 100
Simulating (n,numCCEs) : 17, 105
Simulating (n,numCCEs) : 18, 110
Simulating (n,numCCEs) : 19, 115
Simulating (n,numCCEs) : 20, 120
Simulating (n,numCCEs) : 21, 125
Simulating (n,numCCEs) : 22, 130
Simulating (n,numCCEs) : 23, 135

Compute minimum coreset size for `numUEs` = 15.

[7]:

################
# For 15 UEs
################

numUEs         = 15
rnti           = np.random.choice( np.arange(1,65519+1), size = (numUEs,), replace=False)

probOfBlocking = np.zeros((coresetSize.size,))
for n in range(coresetSize.shape[0]):
    print("Simulating (n,numCCEs) : "+str(n)+", "+str(coresetSize[n]))
    Nccep     = coresetSize[n]
    prob      = 0
    for i in range(numIterations):
        ueALdistribution  = np.random.multinomial(numUEs, aggLevelProbDistribution)
        count             = pdcchSchedulerObj(Nccep,searchSpaceType,ueALdistribution,numCandidates,rnti,strategy)[0]
        numBlockedUEs     = np.sum(count)
        prob              = prob + numBlockedUEs/numUEs
    probOfBlocking[n] = prob/numIterations

targetBlockingProbability   = 0.05
minCoresetSize5ForNumUEs15  = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

targetBlockingProbability   = 0.10
minCoresetSize10ForNumUEs15 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

targetBlockingProbability   = 0.15
minCoresetSize15ForNumUEs15 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

targetBlockingProbability   = 0.20
minCoresetSize20ForNumUEs15 = coresetSize[np.where(probOfBlocking<=targetBlockingProbability)[0][0]]

Simulating (n,numCCEs) : 0, 20
Simulating (n,numCCEs) : 1, 25
Simulating (n,numCCEs) : 2, 30
Simulating (n,numCCEs) : 3, 35
Simulating (n,numCCEs) : 4, 40
Simulating (n,numCCEs) : 5, 45
Simulating (n,numCCEs) : 6, 50
Simulating (n,numCCEs) : 7, 55
Simulating (n,numCCEs) : 8, 60
Simulating (n,numCCEs) : 9, 65
Simulating (n,numCCEs) : 10, 70
Simulating (n,numCCEs) : 11, 75
Simulating (n,numCCEs) : 12, 80
Simulating (n,numCCEs) : 13, 85
Simulating (n,numCCEs) : 14, 90
Simulating (n,numCCEs) : 15, 95
Simulating (n,numCCEs) : 16, 100
Simulating (n,numCCEs) : 17, 105
Simulating (n,numCCEs) : 18, 110
Simulating (n,numCCEs) : 19, 115
Simulating (n,numCCEs) : 20, 120
Simulating (n,numCCEs) : 21, 125
Simulating (n,numCCEs) : 22, 130
Simulating (n,numCCEs) : 23, 135

Display Minimum CORESET size required to meet the Target Blocking Probability for different number of UEs.

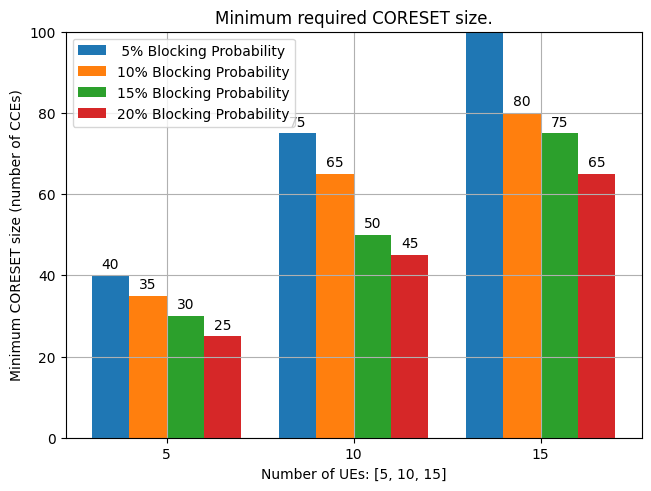
Its the recreation of Fig. 11. Minimum required CORESET size for different number of UEs and blocking probability requirements from the reference paper referenced below [1].
Figure shows that the minimum required CORESET size for 5, 10, 15 UEs and different blocking probability targets of 5%. 10%, 15% and 20%.
Cleary, we see that the CORESET size increases when more UEs are scheduled and a smaller blocking probability target. For instance, comparing two cases:
- case-1: 5 UEs and 20% blocking probability target
- case-2: 10 UEs and 15% blocking probability target
It shows that CORESET size for case-2 needs 3 times larger than that of case-1 (i.e. from 25 CCEs to 75 CCEs).

[8]:

species = ("5", "10", "15")
penguin_means = {' 5% Blocking Probability' : (minCoresetSize5ForNumUEs5,  minCoresetSize5ForNumUEs10,  minCoresetSize5ForNumUEs15),
                 '10% Blocking Probability': (minCoresetSize10ForNumUEs5, minCoresetSize10ForNumUEs10, minCoresetSize10ForNumUEs15),
                 '15% Blocking Probability': (minCoresetSize15ForNumUEs5, minCoresetSize15ForNumUEs10, minCoresetSize15ForNumUEs15),
                 '20% Blocking Probability': (minCoresetSize20ForNumUEs5, minCoresetSize20ForNumUEs10, minCoresetSize20ForNumUEs15)}

x          = np.array([3,8,13]) # the label locations
width      = 1                    # the width of the bars
multiplier = 1

fig, ax = plt.subplots(layout='constrained')

for attribute, measurement in penguin_means.items():
    offset = width * multiplier
    rects = ax.bar(x + offset, measurement, width, label=attribute)
    ax.bar_label(rects, padding=3)
    multiplier += 1

# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_ylabel('Minimum CORESET size (number of CCEs)')
ax.set_xlabel('Number of UEs: [5, 10, 15]')
ax.set_title('Minimum required CORESET size.')
ax.set_xticks(x+2.5, species)
ax.legend(loc='upper left', ncols=1)
ax.set_ylim(0, 100)
ax.grid()
plt.show()

../../../_images/api_Projects_Project2_Minimum_CORESET_Size_for_a_Target_Blocking_Probability_16_0.png

References

[1] Blocking Probability Analysis for 5G New Radio (NR) Physical Downlink Control Channel. Mohammad Mozaffari, Y.-P. Eric Wang, and Kittipong Kittichokechai

[ ]: