Polar Codes in 5G
Polar codes in 5G are used for forward error correction for small to medium payload sizes which is typically the case for broadcast and control channels. The broadcast channel and control channel are used to carry the master information block (MIB) and downlink control information (DCI) repsectively. This tutorial covers the following content:
Table of content:
Import libraries
Python Libraries
[1]:
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
# %matplotlib widget
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes
from mpl_toolkits.axes_grid1.inset_locator import mark_inset
import numpy as np
5G Toolkit libraries
[2]:
# import sys
# sys.path.append("../../../dist2/python3_11/")
import sys
sys.path.append("../../../")
from toolkit5G.SymbolMapping import Demapper
from toolkit5G.SymbolMapping import Mapper
from toolkit5G.ChannelCoder import PolarEncoder5G
from toolkit5G.ChannelCoder import PolarDecoder5G
[3]:
# from IPython.display import display, HTML
# display(HTML("<style>.container { width:70% !important; }</style>"))
Symbol Mapping Configurations
Symbol mapping/Demapping is performed for:
QPSK constellation defined by
constellation_typewhich encodes1 bit per contellation symbol defined by
num_bits_per_symbol.The demapper generates log likelihood ratios configured by
hard_outusing a Log-Map (“app”) decoder defined using
demapping_method.
[4]:
constellation_type = "qam"
num_bits_per_symbol = 2
hard_out = False
demapping_method = "app"
mapper = Mapper(constellation_type, num_bits_per_symbol)
demapper= Demapper(demapping_method, constellation_type, num_bits_per_symbol, hard_out = hard_out)
Polar Coder Configurations
The simulations parameters are:
Kdefines block-length.SNRdBdefines Signal to noise ratio (SNR) in dB.purposedefines the physical channel for which the Polar coder is used.verbosedisplays the details of the simulation if configured to True.decoderTypedefines the type of Polar Decoder used.
[5]:
K = 56 # Number of bits to encode
E = 864 # Rate matching bits
purpose = "PDCCH" # The channel for which the Polar Encoder
verbose = False
decoderType ='SC'
Simulation: AWGN Channel
This subsection performs the simulation which involve following steps:
Bits generation of length
kPolar Encoding
BPSK Symbol Mapping of encoded bits
Passing through the AWGN Channel
Adding noise to BPSK symbols with a given SNR
Symbol De-mapping using Log Map Demapper defined by
"app".Generates Log likelihood values as
hard_outis set toFalse.
Polar Decoding
BER computation
The flow of the implementation can be understood using folowing diagram: 
The bit error rate (BER) is computed for every combination of K \(= \{20, 50, 80, 110, 140\}\) and SNR \(= \{-10, -8, -6, -4, -2, 0\}\) dB and averaged over \(500000\) batches (monteCarloIterations).
[6]:
K = np.int32(np.linspace(20,140,5))
SNRdB = np.linspace(-10,0,5)
SNR = 10**(SNRdB/10)
numBatches = 100
BER = np.zeros((K.size, SNR.size))
kIndex = 0
snrIndex = 0
for k in K:
#######################################################
################ Generate UCI Payload #################
#######################################################
bits = np.float32(np.random.randint(2, size = (numBatches, k)))
#######################################################
################### Polar Encoder #####################
#######################################################
encoder = PolarEncoder5G(k, E, purpose,verbose)
encBits = encoder(bits)
#######################################################
################### Rate Matching #####################
#######################################################
encoder = PolarEncoder5G(k, E, purpose,verbose)
#######################################################
################### Symbol Mapping ####################
#######################################################
symbols = mapper(encBits)
decoder = PolarDecoder5G(K = k, E = E, purpose = purpose, dec_type = decoderType)
snrIndex = 0
for snr in SNR:
#######################################################
################ Add Noise at Receiver ################
#######################################################
symbs = symbols + np.sqrt(0.5/snr)*(np.random.standard_normal(size=symbols.shape)+1j*np.random.standard_normal(size=symbols.shape)).astype(np.complex64)
#######################################################
################## Symbol Demapping ###################
#######################################################
llrEst = demapper([symbs, np.float32(1/snr)])
#######################################################
################ Reed Muller Decoder ##################
#######################################################
rxBits = decoder(llrEst)
#######################################################
############## Key Performance Metrics ################
#######################################################
BER[kIndex, snrIndex] = np.mean(np.abs(rxBits-bits))
print("For K="+str(k)+", At SNR(dB): "+str(SNRdB[snrIndex])+" | Bit Error Rate: "+str(BER[kIndex, snrIndex]))
snrIndex = snrIndex + 1
kIndex = kIndex + 1
Warning: 5G Polar codes use an integrated CRC that cannot be materialized with SC decoding and, thus, causes a degraded performance. Please consider SCL decoding instead.
For K=20, At SNR(dB): -10.0 | Bit Error Rate: 0.27399998903274536
For K=20, At SNR(dB): -7.5 | Bit Error Rate: 0.08749999850988388
For K=20, At SNR(dB): -5.0 | Bit Error Rate: 0.0020000000949949026
For K=20, At SNR(dB): -2.5 | Bit Error Rate: 0.0
For K=20, At SNR(dB): 0.0 | Bit Error Rate: 0.0
Warning: 5G Polar codes use an integrated CRC that cannot be materialized with SC decoding and, thus, causes a degraded performance. Please consider SCL decoding instead.
For K=50, At SNR(dB): -10.0 | Bit Error Rate: 0.4251999855041504
For K=50, At SNR(dB): -7.5 | Bit Error Rate: 0.17100000381469727
For K=50, At SNR(dB): -5.0 | Bit Error Rate: 0.00559999980032444
For K=50, At SNR(dB): -2.5 | Bit Error Rate: 0.0
For K=50, At SNR(dB): 0.0 | Bit Error Rate: 0.0
Warning: 5G Polar codes use an integrated CRC that cannot be materialized with SC decoding and, thus, causes a degraded performance. Please consider SCL decoding instead.
For K=80, At SNR(dB): -10.0 | Bit Error Rate: 0.48124998807907104
For K=80, At SNR(dB): -7.5 | Bit Error Rate: 0.453000009059906
For K=80, At SNR(dB): -5.0 | Bit Error Rate: 0.18912500143051147
For K=80, At SNR(dB): -2.5 | Bit Error Rate: 0.004999999888241291
For K=80, At SNR(dB): 0.0 | Bit Error Rate: 0.0
Warning: 5G Polar codes use an integrated CRC that cannot be materialized with SC decoding and, thus, causes a degraded performance. Please consider SCL decoding instead.
For K=110, At SNR(dB): -10.0 | Bit Error Rate: 0.48818182945251465
For K=110, At SNR(dB): -7.5 | Bit Error Rate: 0.4808181822299957
For K=110, At SNR(dB): -5.0 | Bit Error Rate: 0.42027273774147034
For K=110, At SNR(dB): -2.5 | Bit Error Rate: 0.049272727221250534
For K=110, At SNR(dB): 0.0 | Bit Error Rate: 0.0
Warning: 5G Polar codes use an integrated CRC that cannot be materialized with SC decoding and, thus, causes a degraded performance. Please consider SCL decoding instead.
For K=140, At SNR(dB): -10.0 | Bit Error Rate: 0.49235713481903076
For K=140, At SNR(dB): -7.5 | Bit Error Rate: 0.4894285798072815
For K=140, At SNR(dB): -5.0 | Bit Error Rate: 0.47942855954170227
For K=140, At SNR(dB): -2.5 | Bit Error Rate: 0.24899999797344208
For K=140, At SNR(dB): 0.0 | Bit Error Rate: 0.004142857156693935
Performance Evaluations
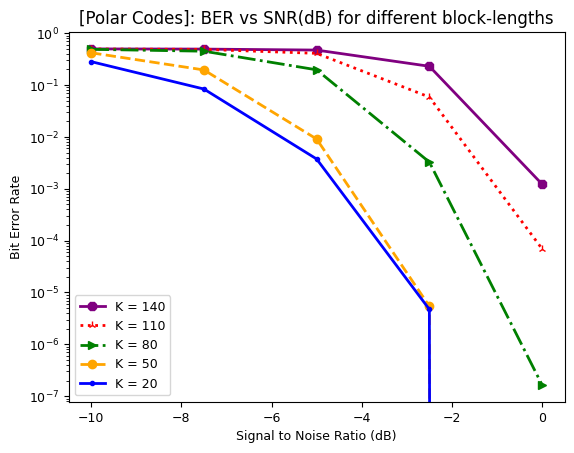
The script plots SNR in dB vs BER performance for different code-block lengths \(\text{K} \in \{20, 50, 80, 110, 140\}\). It can be observed that the Polar codes can provide the reliablilty of
\(99.99990 \text{ or BER = } 10^{-4}\) for all the block-sizes supported in downlink even at low SNR value of 0 dB.
[7]:
fig, ax = plt.subplots()
color_tuple = ['blue', 'orange', 'green', 'red', 'purple', 'brown', 'pink', 'gray', 'olive', 'cyan', 'black']
markcolor_tuple = ['gold', 'navy', 'crimson', 'yellow', 'line', 'springgreen', 'black', 'aqua', 'royalblue', 'red', 'green']
linestyle_tuple = ['-', '--', '-.', ':', 'solid', 'dashed', 'dashdot', 'dotted']
marker_tuple = [".", "o", ">", "2", "8", "s", "p", "*", "P", "X", "D"]
kIndex = K.size-1
for k in np.flip(K):
ax.semilogy(SNRdB, BER[kIndex], color=color_tuple[kIndex%len(color_tuple)],
linestyle=linestyle_tuple[kIndex%len(linestyle_tuple)], lw = 2,
marker=marker_tuple[kIndex%len(marker_tuple)], markersize = 6, label="K = "+str(k))
kIndex = kIndex - 1
ax.legend(loc="lower left")
ax.set_xlabel("Signal to Noise Ratio (dB)", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("[Polar Codes]: BER vs SNR(dB) for different block-lengths", fontsize = 12)
plt.rcParams.update({'font.size': 9})
plt.show()
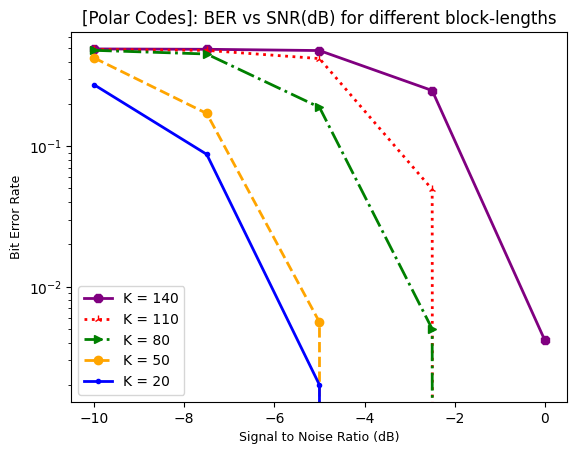
Performance Evaluations: Averaging over a 100 dataset of 100 points each
[8]:
BER = np.zeros((K.size, SNR.size))
for i in range(100):
ds = np.load("Databases/Polar_BERvsSNR"+str(i)+".npz")
BER = BER + ds['BER']
BER = BER/100
fig, ax = plt.subplots()
color_tuple = ['blue', 'orange', 'green', 'red', 'purple', 'brown', 'pink', 'gray', 'olive', 'cyan', 'black']
markcolor_tuple = ['gold', 'navy', 'crimson', 'yellow', 'line', 'springgreen', 'black', 'aqua', 'royalblue', 'red', 'green']
linestyle_tuple = ['-', '--', '-.', ':', 'solid', 'dashed', 'dashdot', 'dotted']
marker_tuple = [".", "o", ">", "2", "8", "s", "p", "*", "P", "X", "D"]
kIndex = K.size-1
for k in np.flip(K):
ax.semilogy(SNRdB, BER[kIndex], color=color_tuple[kIndex%len(color_tuple)],
linestyle=linestyle_tuple[kIndex%len(linestyle_tuple)], lw = 2,
marker=marker_tuple[kIndex%len(marker_tuple)], markersize = 6, label="K = "+str(k))
kIndex = kIndex - 1
ax.legend(loc="lower left")
ax.set_xlabel("Signal to Noise Ratio (dB)", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("[Polar Codes]: BER vs SNR(dB) for different block-lengths", fontsize = 12)
plt.rcParams.update({'font.size': 9})
plt.show()
[ ]: