Learning to Demap
This notebook introduces the users to few functionalities provided by the 5G Toolkit such as
PDSCH Transmitter Chain
PDSCH Receiver
Symbol Demapper.
The PDSCH transmitter is compliant with 5G standards defined in 38.211, 38.212 and 38.214. Finally, the tutorial will teach the user to replace one of the PDSCH receiver’s module called Symbol Demapper with a neural network based Symbol Demapper (LLRNet).
Conventional Techniques
- Log MAP Demapper
- Optimal for AWGN Noise ==> Highest possible data rate | Lowest possible Block error rate
- Complexity: Combinatorial ==> Consumes a lot of power
- Not suitable for Internet of Things (**IoT**) devices.
- Max log MAP Demapper
- Sub-Optimal performance ==> 3 dB loss in performance
- Complexity: Linear ==> Consumes a less power compared to log-MAP
Proposed Techniques
- LLRNet
- B(L)ER and Throughput Performance matches Log MAP Demapper
- Complexity: Even lower than Max log MAP Demapper
Finally, the user will be able to rapidly evaluate and compare the
Bit Error rate vs SNR
Block Error rate vs SNR
Throughput/Data rate vs SNR
Computational Complexity of Log-MAP, Max-Log-MAP and LLRNet methods.
Table of Contents
Import Libraries
Import Python Libraries
[1]:
# %matplotlib inline
# %matplotlib notebook
# %matplotlib widget
import matplotlib.pyplot as plt
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
Import 5G Toolkit Modules
[2]:
from llrNet import LLRNet
from toolkit5G.SymbolMapping import Demapper
from toolkit5G.SymbolMapping import Mapper
[3]:
# from IPython.display import display, HTML
# display(HTML("<style>.container { width:70% !important; }</style>"))
Learning to Demap the Symbols
The Mapping between input and output is learned for a specific modulation order at a given SNR. The neural network model used for learning looks as follows:
The following inputs are expected for the experiments
modOrder: Defines the modulation order.nodesPerLayer: Defines the number of nodes used for hidden layers. Number of nodes for input layer is 2 and number of nodes at the output layer ismodOrder. Number of hidden layers = np.size(nodesPerLayer).activationfunctions: Defines the activation function used for each layer. Length should equal to np.size(nodesPerLayer) + 1. The last value defines the activation function for the output layer.numTrainingSamples: Defines the number of samples used for training the model.numTestSamples: Defines the number of samples used for testing the performance of the model.SNR: SNR value.
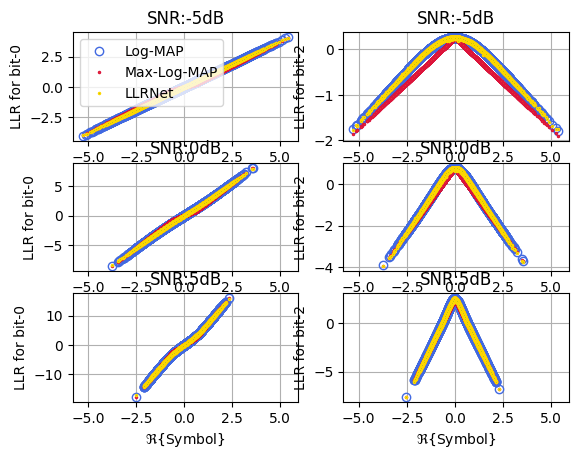
Input Output Mapping for M = 4
[4]:
modOrder = int(np.random.choice([2,4,6,8,10]))
nodesPerLayer = np.array([32, 64, 32])
activationfunctions = np.array(['relu', 'relu', 'relu', 'linear'])
numTrainingSamples = 2**16
llrNet = LLRNet(modOrder = modOrder, nodesPerLayer = nodesPerLayer,
numTrainingSamples = numTrainingSamples, activationfunctions = activationfunctions)
plt1, fig, ax = llrNet.displayMapping(modOrder = 4, bitLocations = [0,2], SNRdB = [-5,0,5],
numSamples = 2**16, displayRealPart = True)
************************************ Training the Model ***********************************
...........................................................................................
*********************************** Evaluating the Model **********************************
...........................................................................................
512/512 [==============================] - 0s 424us/step - loss: 5.0708e-05 - accuracy: 0.9950
Training Accuracy: 99.50
512/512 [==============================] - 0s 379us/step
************************************ Training the Model ***********************************
...........................................................................................
*********************************** Evaluating the Model **********************************
...........................................................................................
512/512 [==============================] - 0s 416us/step - loss: 3.4907e-04 - accuracy: 0.9951
Training Accuracy: 99.51
512/512 [==============================] - 0s 363us/step
************************************ Training the Model ***********************************
...........................................................................................
*********************************** Evaluating the Model **********************************
...........................................................................................
512/512 [==============================] - 0s 416us/step - loss: 0.0027 - accuracy: 0.9924
Training Accuracy: 99.24
512/512 [==============================] - 0s 394us/step
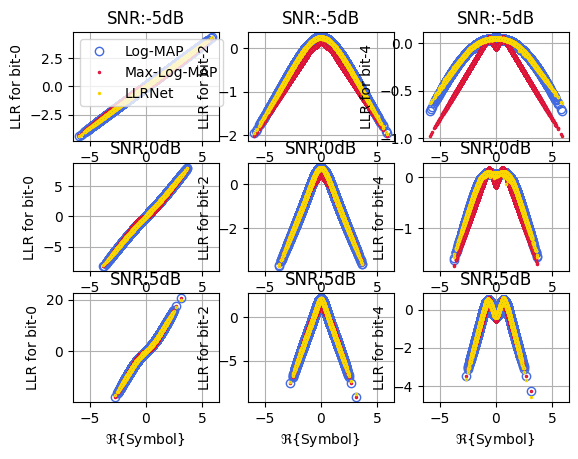
Input Output Mapping for M = 6
[5]:
modOrder = int(np.random.choice([2,4,6,8,10]))
nodesPerLayer = np.array([32, 64, 32])
activationfunctions = np.array(['relu', 'relu', 'relu', 'linear'])
numTrainingSamples = 2**16
SNR = 10
llrNet = LLRNet(modOrder = modOrder, nodesPerLayer = nodesPerLayer,
numTrainingSamples = numTrainingSamples, activationfunctions = activationfunctions)
plt1, fig, ax = llrNet.displayMapping(modOrder = 6, bitLocations = [0,2,4], SNRdB = [-5,0,5],
numSamples = 3*2**18, displayRealPart = True)
************************************ Training the Model ***********************************
...........................................................................................
*********************************** Evaluating the Model **********************************
...........................................................................................
4096/4096 [==============================] - 2s 431us/step - loss: 1.3449e-05 - accuracy: 0.9889
Training Accuracy: 98.89
4096/4096 [==============================] - 2s 404us/step
************************************ Training the Model ***********************************
...........................................................................................
*********************************** Evaluating the Model **********************************
...........................................................................................
4096/4096 [==============================] - 2s 427us/step - loss: 2.1801e-04 - accuracy: 0.9898
Training Accuracy: 98.98
4096/4096 [==============================] - 2s 411us/step
************************************ Training the Model ***********************************
...........................................................................................
*********************************** Evaluating the Model **********************************
...........................................................................................
4096/4096 [==============================] - 2s 408us/step - loss: 5.5913e-04 - accuracy: 0.9932
Training Accuracy: 99.32
4096/4096 [==============================] - 2s 385us/step
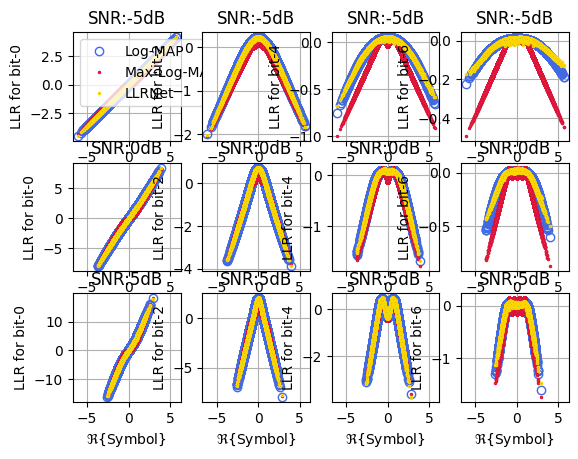
Input Output Mapping for M = 8
[6]:
modOrder = int(np.random.choice([2,4,6,8,10]))
nodesPerLayer = np.array([32, 64, 32])
activationfunctions = np.array(['relu', 'relu', 'relu', 'linear'])
numTrainingSamples = 2**16
SNR = 10
llrNet = LLRNet(modOrder = modOrder, nodesPerLayer = nodesPerLayer,
numTrainingSamples = numTrainingSamples, activationfunctions = activationfunctions)
plt1, fig, ax = llrNet.displayMapping(modOrder = 8, bitLocations = [0,2,4,6], SNRdB = [-5,0,5],
numSamples = 2**20, displayRealPart = True)
************************************ Training the Model ***********************************
...........................................................................................
*********************************** Evaluating the Model **********************************
...........................................................................................
4096/4096 [==============================] - 2s 420us/step - loss: 2.3101e-05 - accuracy: 0.9636
Training Accuracy: 96.36
4096/4096 [==============================] - 2s 366us/step
************************************ Training the Model ***********************************
...........................................................................................
*********************************** Evaluating the Model **********************************
...........................................................................................
4096/4096 [==============================] - 2s 421us/step - loss: 1.5198e-04 - accuracy: 0.9639
Training Accuracy: 96.39
4096/4096 [==============================] - 2s 369us/step
************************************ Training the Model ***********************************
...........................................................................................
*********************************** Evaluating the Model **********************************
...........................................................................................
4096/4096 [==============================] - 2s 435us/step - loss: 3.2795e-04 - accuracy: 0.9872
Training Accuracy: 98.72
4096/4096 [==============================] - 2s 395us/step
Throughput and BER Performance of LLRnet
Import Libraries
[7]:
from toolkit5G.PhysicalChannels.PDSCH import ComputeTransportBlockSize
from toolkit5G.PhysicalChannels import PDSCHLowerPhy
from toolkit5G.PhysicalChannels import PDSCHDecoderLowerPhy
from toolkit5G.PhysicalChannels import PDSCHUpperPhy
from toolkit5G.PhysicalChannels import PDSCHDecoderUpperPhy
from toolkit5G.Configurations import TimeFrequency5GParameters
from toolkit5G.ChannelProcessing import AddNoise
Simulation Parameters
Parameters |
Variable |
Values |
|---|---|---|
Number of frames |
|
200 |
Subcarrier Spacing |
|
30 KHz |
Bandwidth |
|
20 MHz |
Number of Resource Blocks |
|
51 |
Number of Transmit Antennas |
|
8 |
Number of Receive Antennas |
|
2 |
Number of layers |
|
2 |
Physical Channel |
|
Simulation are carried out for Physical Downlink Shared Channel (PDSCH) |
Channel Coder |
|
PDSCH uses Low density parity check codes internally |
Code rate |
|
0.4785 |
Modulation Order |
|
16-QAM, 64-QAM, 256–QAM |
[8]:
# Simulation Parameters
numBSs = 1
numUEs = 1
numFrames = 1
scSpacing = 30000
Bandwidth = 20*10**6
nSymbolFrame = 140*int(scSpacing/15000); # Number of OFDM symbols per frame (Its a function of subcarrier spacing)
slotDuration = 0.001/(scSpacing/15000)
tfParams = TimeFrequency5GParameters(Bandwidth, scSpacing)
tfParams(nSymbolFrame, typeCP = "normal")
numRBs = tfParams.N_RB
# Antenna and Precoding Parameters
numTx = 8
numRx = 2
numLayers = 2
PDSCH Parameters
[9]:
# Set start symbol and number of symbols for DMRS transmission.
startSymbol = 0
numSymbols = 13
dmrsREs = 0
scalingField = '00'
# Modulation and Coding Rate Parameters
codeRate = 0.4785
modOrders = [4, 6, 8] ## For 16-QAM, 64-QAM and 256-QAM
numLayers = 2
numTBs = 1
additionalOverhead = 0
print("************ PDSCH Parameters *************")
print()
print(" startSymbol: "+str(startSymbol))
print(" numSymbols: "+str(numSymbols))
print(" dmrsREs: "+str(dmrsREs))
print(" scalingField: "+str(scalingField))
print(" modOrder: "+str(modOrders))
print(" codeRate: "+str(codeRate))
print(" numLayers: "+str(numLayers))
print(" numTBs: "+str(numTBs))
print(" additionalOverhead: "+str(additionalOverhead))
print()
print("********************************************")
enableLBRM = False # Flag to enable/disbale "Limited buffer rate matching"
rvid1 = 0 # Redundency version-ID for TB-1: As per 3GPP TS38.212
rvid2 = 0 # Redundency version-ID for TB-2: As per 3GPP TS38.212
************ PDSCH Parameters *************
startSymbol: 0
numSymbols: 13
dmrsREs: 0
scalingField: 00
modOrder: [4, 6, 8]
codeRate: 0.4785
numLayers: 2
numTBs: 1
additionalOverhead: 0
********************************************
LLRnet Parameters
Training Framework
The artificial neural network (ANN) is trained to mimic a optimal method with lower complexity.
The input to ANN model and optimal log-MAP method is the estimated equalized symbol and the output of the log-MAP method is fed to ANN output for learning the model parameters using adaptive moment estimation (ADAM) optimizer while Levenberg-Marquardt backpropagation.
We are assuming
epochs= 4,batch_size= 32 for reasonable complexing while training.Note: We are assuming slighly large neural networks compared to what paper claims. As we were unable to reproduce the exact same results.
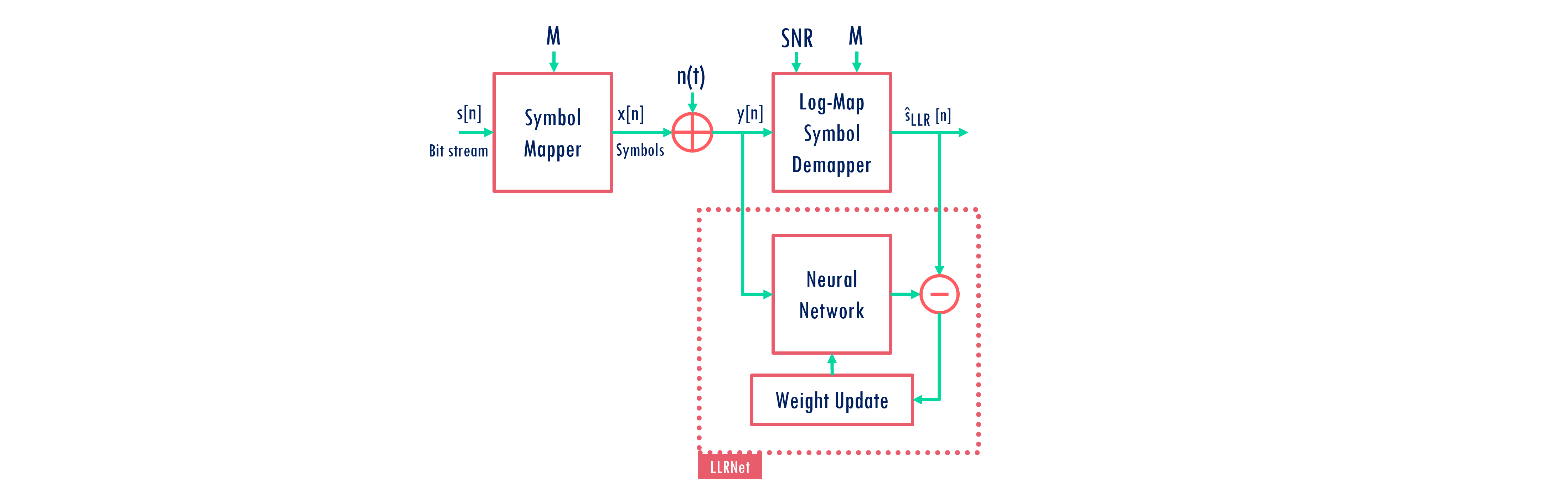
Deployment Framework
The trained model is used to predict the llr for each bits for the received symbols.
The received symbol is represented using the its real and imaginary part and fed to the model.
The ANN model emits
M-llr estimates one for each bit.

[10]:
nodesPerLayer = np.array([32, 64, 32])
activationfunctions = np.array(['relu', 'relu', 'relu', 'linear'])
numTrainingSamples = 3*2**18
Simulation Section
The simulation is carried out for 3 modulation orders 16-QAM (M=4), 64-QAM (M=6), and 256-QAM (M=8).
For M = 4:
The simulation is carried out for SNR (dB) in the range ().
For M = 6:
The simulation is carried out for SNR (dB) in the range ().
For M = 8:
The simulation is carried out for SNR (dB) in the range ().
[11]:
modOrders = np.array([4, 6, 8]) ## For 16-QAM, 64-QAM and 256-QAM
numPoints = 3
SNRdB = np.array([np.linspace(5.4, 6.4, numPoints),
np.linspace(9.5, 10.8, numPoints),
np.linspace(13.4, 14.4, numPoints)])
BER = np.zeros((3, modOrders.size, SNRdB.shape[-1]))
BLER = np.zeros((3, modOrders.size, SNRdB.shape[-1]))
Throughput = np.zeros((3, modOrders.size, SNRdB.shape[-1]))
SNR = 10**(0.1*SNRdB)
maxThroughput = (14*numRBs*12*modOrders*numLayers*codeRate)/slotDuration
mcsIdx = 0
for modorder in modOrders:
## PDSCH-transmitter chain object
pdschUpPhy = PDSCHUpperPhy(numTBs = numTBs, mcsIndex = np.array([modorder, codeRate]),
symbolsPerSlot = numSymbols, numRB = numRBs,
numlayers = [numLayers], scalingField = scalingField,
additionalOverhead = additionalOverhead, dmrsREs = dmrsREs,
pdschTable = None, verbose=False)
codewords = pdschUpPhy(rvid = [rvid1, rvid2], enableLBRM = [False, False],
numBatch = numFrames, numBSs = numBSs)
symbols = Mapper("qam", pdschUpPhy.modOrder)(codewords[0])
snrIndex = 0
for snr in SNR[mcsIdx]:
# log-MAP Decoder
rxSymbols = np.complex64(AddNoise()(symbols, 1/snr))
llrs = Demapper("app", "qam", int(modorder), hard_out = False)([rxSymbols, np.float32(1/snr)])
# Receiver: Upper Physical layer
pdschDecoderUpperPhy = PDSCHDecoderUpperPhy(numTBs, np.array([modorder, codeRate]), numSymbols,
numRBs, [numLayers], scalingField,
additionalOverhead, dmrsREs,
enableLBRM=[False, False], pdschTable=None,
rvid=[rvid1], verbose=False)
tbEst = pdschDecoderUpperPhy([llrs])
BER[0, mcsIdx, snrIndex] = np.mean(np.abs(tbEst[0] - pdschUpPhy.tblock1))
if (pdschDecoderUpperPhy.numCBs == 1):
BLER[0, mcsIdx, snrIndex] = 1 - np.mean(pdschDecoderUpperPhy.crcCheckTBs)
else:
BLER[0, mcsIdx, snrIndex] = 1 - np.mean(pdschDecoderUpperPhy.crcCheckforCBs)
Throughput[0, mcsIdx, snrIndex] = (1-BLER[0, mcsIdx, snrIndex])*pdschUpPhy.tblock1.shape[-1]/slotDuration
print()
print("+++++++++++ [ snrIndex: "+str(snrIndex)+" | modorder: "+str(modorder)+"] +++++++++++")
print("===================================================")
print(" **************** log-MAP **************** ")
print("mod-Order: "+str(modorder)+" | SNR (dB): "+str(SNRdB[mcsIdx, snrIndex]))
print(" BER: "+str(BER[0, mcsIdx, snrIndex]))
print(" BLER: "+str(BLER[0, mcsIdx, snrIndex]))
print(" Throughput: "+str(Throughput[0, mcsIdx, snrIndex]))
print(".......................................................")
# max-log-MAP Decoder
llrs = Demapper("maxlog", "qam", int(modorder), hard_out = False)([rxSymbols, np.float32(1/snr)])
pdschDecoderUpperPhy = PDSCHDecoderUpperPhy(numTBs, np.array([modorder, codeRate]), numSymbols,
numRBs, [numLayers], scalingField,
additionalOverhead, dmrsREs,
enableLBRM=[False, False], pdschTable=None,
rvid=[rvid1], verbose=False)
tbEst = pdschDecoderUpperPhy([llrs])
BER[1, mcsIdx, snrIndex] = np.mean(np.abs(tbEst[0] - pdschUpPhy.tblock1))
if (pdschDecoderUpperPhy.numCBs == 1):
BLER[1, mcsIdx, snrIndex] = 1 - np.mean(pdschDecoderUpperPhy.crcCheckTBs)
else:
BLER[1, mcsIdx, snrIndex] = 1 - np.mean(pdschDecoderUpperPhy.crcCheckforCBs)
Throughput[1, mcsIdx, snrIndex] = (1-BLER[1, mcsIdx, snrIndex])*pdschUpPhy.tblock1.shape[-1]/slotDuration
print(" **************** max-log-MAP **************** ")
print("mod-Order: "+str(modorder)+" | SNR (dB): "+str(SNRdB[mcsIdx, snrIndex]))
print(" BER: "+str(BER[1, mcsIdx, snrIndex]))
print(" BLER: "+str(BLER[1, mcsIdx, snrIndex]))
print(" Throughput: "+str(Throughput[1, mcsIdx, snrIndex]))
print(".......................................................")
llrNet = LLRNet(modOrder = int(modorder), nodesPerLayer = nodesPerLayer,
numTrainingSamples = numTrainingSamples, activationfunctions = activationfunctions)
llrs = llrNet(snr, rxSymbols)
# Receiver: Upper Physical layer
pdschDecoderUpperPhy = PDSCHDecoderUpperPhy(numTBs, np.array([modorder, codeRate]), numSymbols,
numRBs, [numLayers], scalingField,
additionalOverhead, dmrsREs,
enableLBRM=[False, False], pdschTable=None,
rvid=[rvid1], verbose=False)
tbEst = pdschDecoderUpperPhy([llrs])
BER[2, mcsIdx, snrIndex] = np.mean(np.abs(tbEst[0] - pdschUpPhy.tblock1))
if (pdschDecoderUpperPhy.numCBs == 1):
BLER[2, mcsIdx, snrIndex] = 1 - np.mean(pdschDecoderUpperPhy.crcCheckTBs)
else:
BLER[2, mcsIdx, snrIndex] = 1 - np.mean(pdschDecoderUpperPhy.crcCheckforCBs)
Throughput[2, mcsIdx, snrIndex] = (1-BLER[2, mcsIdx, snrIndex])*pdschUpPhy.tblock1.shape[-1]/slotDuration
print(" ******************* LLRnet ****************** ")
print("mod-Order: "+str(modorder)+" | SNR (dB): "+str(SNRdB[mcsIdx, snrIndex]))
print(" BER: "+str(BER[2, mcsIdx, snrIndex]))
print(" BLER: "+str(BLER[2, mcsIdx, snrIndex]))
print(" Throughput: "+str(Throughput[2, mcsIdx, snrIndex]))
print("_______________________________________________________")
print()
snrIndex += 1
mcsIdx += 1
+++++++++++ [ snrIndex: 0 | modorder: 4] +++++++++++
===================================================
**************** log-MAP ****************
mod-Order: 4 | SNR (dB): 5.4
BER: 0.03322742917659518
BLER: 1.0
Throughput: 0.0
.......................................................
**************** max-log-MAP ****************
mod-Order: 4 | SNR (dB): 5.4
BER: 0.03650383902568176
BLER: 1.0
Throughput: 0.0
.......................................................
************************************ Training the Model ***********************************
...........................................................................................
Epoch 1/4
24576/24576 [==============================] - 14s 558us/step - loss: 0.0532 - accuracy: 0.9940
Epoch 2/4
24576/24576 [==============================] - 14s 560us/step - loss: 5.3267e-04 - accuracy: 0.9973
Epoch 3/4
24576/24576 [==============================] - 14s 570us/step - loss: 3.9570e-04 - accuracy: 0.9978
Epoch 4/4
24576/24576 [==============================] - 13s 547us/step - loss: 3.2879e-04 - accuracy: 0.9981
*********************************** Evaluating the Model **********************************
...........................................................................................
24576/24576 [==============================] - 11s 436us/step - loss: 1.6346e-04 - accuracy: 0.9985
Training Accuracy: 99.85
498/498 [==============================] - 0s 412us/step
******************* LLRnet ******************
mod-Order: 4 | SNR (dB): 5.4
BER: 0.03312814402965317
BLER: 1.0
Throughput: 0.0
_______________________________________________________
+++++++++++ [ snrIndex: 1 | modorder: 4] +++++++++++
===================================================
**************** log-MAP ****************
mod-Order: 4 | SNR (dB): 5.9
BER: 0.0043023563674874235
BLER: 0.75
Throughput: 15108000.0
.......................................................
**************** max-log-MAP ****************
mod-Order: 4 | SNR (dB): 5.9
BER: 0.004335451416468097
BLER: 1.0
Throughput: 0.0
.......................................................
************************************ Training the Model ***********************************
...........................................................................................
Epoch 1/4
24576/24576 [==============================] - 14s 553us/step - loss: 0.0604 - accuracy: 0.9941
Epoch 2/4
24576/24576 [==============================] - 14s 559us/step - loss: 5.5362e-04 - accuracy: 0.9978
Epoch 3/4
24576/24576 [==============================] - 14s 554us/step - loss: 4.4147e-04 - accuracy: 0.9981
Epoch 4/4
24576/24576 [==============================] - 14s 557us/step - loss: 4.0288e-04 - accuracy: 0.9982
*********************************** Evaluating the Model **********************************
...........................................................................................
24576/24576 [==============================] - 11s 437us/step - loss: 3.2303e-04 - accuracy: 0.9984
Training Accuracy: 99.84
498/498 [==============================] - 0s 394us/step
******************* LLRnet ******************
mod-Order: 4 | SNR (dB): 5.9
BER: 0.004136881122584061
BLER: 0.75
Throughput: 15108000.0
_______________________________________________________
+++++++++++ [ snrIndex: 2 | modorder: 4] +++++++++++
===================================================
**************** log-MAP ****************
mod-Order: 4 | SNR (dB): 6.4
BER: 0.0
BLER: 0.0
Throughput: 60432000.0
.......................................................
**************** max-log-MAP ****************
mod-Order: 4 | SNR (dB): 6.4
BER: 0.0
BLER: 0.0
Throughput: 60432000.0
.......................................................
************************************ Training the Model ***********************************
...........................................................................................
Epoch 1/4
24576/24576 [==============================] - 14s 571us/step - loss: 0.0685 - accuracy: 0.9942
Epoch 2/4
24576/24576 [==============================] - 14s 562us/step - loss: 7.1901e-04 - accuracy: 0.9975
Epoch 3/4
24576/24576 [==============================] - 13s 544us/step - loss: 5.8154e-04 - accuracy: 0.9977
Epoch 4/4
24576/24576 [==============================] - 13s 535us/step - loss: 5.1438e-04 - accuracy: 0.9979
*********************************** Evaluating the Model **********************************
...........................................................................................
24576/24576 [==============================] - 11s 430us/step - loss: 3.2593e-04 - accuracy: 0.9986
Training Accuracy: 99.86
498/498 [==============================] - 0s 376us/step
******************* LLRnet ******************
mod-Order: 4 | SNR (dB): 6.4
BER: 0.0
BLER: 0.0
Throughput: 60432000.0
_______________________________________________________
+++++++++++ [ snrIndex: 0 | modorder: 6] +++++++++++
===================================================
**************** log-MAP ****************
mod-Order: 6 | SNR (dB): 9.5
BER: 0.04819538434842964
BLER: 1.0
Throughput: 0.0
.......................................................
**************** max-log-MAP ****************
mod-Order: 6 | SNR (dB): 9.5
BER: 0.0575438139857713
BLER: 1.0
Throughput: 0.0
.......................................................
************************************ Training the Model ***********************************
...........................................................................................
Epoch 1/4
24576/24576 [==============================] - 14s 564us/step - loss: 0.1990 - accuracy: 0.9810
Epoch 2/4
24576/24576 [==============================] - 14s 561us/step - loss: 0.0030 - accuracy: 0.9943
Epoch 3/4
24576/24576 [==============================] - 14s 558us/step - loss: 0.0022 - accuracy: 0.9947
Epoch 4/4
24576/24576 [==============================] - 14s 583us/step - loss: 0.0017 - accuracy: 0.9955
*********************************** Evaluating the Model **********************************
...........................................................................................
24576/24576 [==============================] - 11s 453us/step - loss: 0.0012 - accuracy: 0.9955
Training Accuracy: 99.55
498/498 [==============================] - 0s 402us/step
******************* LLRnet ******************
mod-Order: 6 | SNR (dB): 9.5
BER: 0.048759326739545375
BLER: 1.0
Throughput: 0.0
_______________________________________________________
+++++++++++ [ snrIndex: 1 | modorder: 6] +++++++++++
===================================================
**************** log-MAP ****************
mod-Order: 6 | SNR (dB): 10.15
BER: 0.0028630921395106715
BLER: 0.6666666666666667
Throughput: 30735999.999999993
.......................................................
**************** max-log-MAP ****************
mod-Order: 6 | SNR (dB): 10.15
BER: 0.0068974492451847995
BLER: 1.0
Throughput: 0.0
.......................................................
************************************ Training the Model ***********************************
...........................................................................................
Epoch 1/4
24576/24576 [==============================] - 14s 573us/step - loss: 0.2472 - accuracy: 0.9827
Epoch 2/4
24576/24576 [==============================] - 14s 555us/step - loss: 0.0027 - accuracy: 0.9948
Epoch 3/4
24576/24576 [==============================] - 14s 556us/step - loss: 0.0021 - accuracy: 0.9955
Epoch 4/4
24576/24576 [==============================] - 14s 572us/step - loss: 0.0018 - accuracy: 0.9956
*********************************** Evaluating the Model **********************************
...........................................................................................
24576/24576 [==============================] - 11s 437us/step - loss: 0.0015 - accuracy: 0.9960
Training Accuracy: 99.60
498/498 [==============================] - 0s 400us/step
******************* LLRnet ******************
mod-Order: 6 | SNR (dB): 10.15
BER: 0.002732951587714732
BLER: 0.6666666666666667
Throughput: 30735999.999999993
_______________________________________________________
+++++++++++ [ snrIndex: 2 | modorder: 6] +++++++++++
===================================================
**************** log-MAP ****************
mod-Order: 6 | SNR (dB): 10.8
BER: 0.0
BLER: 0.0
Throughput: 92208000.0
.......................................................
**************** max-log-MAP ****************
mod-Order: 6 | SNR (dB): 10.8
BER: 0.0
BLER: 0.0
Throughput: 92208000.0
.......................................................
************************************ Training the Model ***********************************
...........................................................................................
Epoch 1/4
24576/24576 [==============================] - 14s 544us/step - loss: 0.3719 - accuracy: 0.9796
Epoch 2/4
24576/24576 [==============================] - 13s 545us/step - loss: 0.0041 - accuracy: 0.9942
Epoch 3/4
24576/24576 [==============================] - 13s 541us/step - loss: 0.0033 - accuracy: 0.9952
Epoch 4/4
24576/24576 [==============================] - 14s 579us/step - loss: 0.0027 - accuracy: 0.9956
*********************************** Evaluating the Model **********************************
...........................................................................................
24576/24576 [==============================] - 11s 442us/step - loss: 0.0028 - accuracy: 0.9960
Training Accuracy: 99.60
498/498 [==============================] - 0s 397us/step
******************* LLRnet ******************
mod-Order: 6 | SNR (dB): 10.8
BER: 0.0
BLER: 0.0
Throughput: 92208000.0
_______________________________________________________
+++++++++++ [ snrIndex: 0 | modorder: 8] +++++++++++
===================================================
**************** log-MAP ****************
mod-Order: 8 | SNR (dB): 13.4
BER: 0.025853513298928148
BLER: 1.0
Throughput: 0.0
.......................................................
**************** max-log-MAP ****************
mod-Order: 8 | SNR (dB): 13.4
BER: 0.03868929469366151
BLER: 1.0
Throughput: 0.0
.......................................................
************************************ Training the Model ***********************************
...........................................................................................
Epoch 1/4
24576/24576 [==============================] - 14s 541us/step - loss: 0.7246 - accuracy: 0.9726
Epoch 2/4
24576/24576 [==============================] - 14s 562us/step - loss: 0.0133 - accuracy: 0.9930
Epoch 3/4
24576/24576 [==============================] - 14s 571us/step - loss: 0.0117 - accuracy: 0.9936
Epoch 4/4
24576/24576 [==============================] - 14s 558us/step - loss: 0.0101 - accuracy: 0.9936
*********************************** Evaluating the Model **********************************
...........................................................................................
24576/24576 [==============================] - 11s 442us/step - loss: 0.0095 - accuracy: 0.9938
Training Accuracy: 99.38
498/498 [==============================] - 0s 386us/step
******************* LLRnet ******************
mod-Order: 8 | SNR (dB): 13.4
BER: 0.027838427947598252
BLER: 1.0
Throughput: 0.0
_______________________________________________________
+++++++++++ [ snrIndex: 1 | modorder: 8] +++++++++++
===================================================
**************** log-MAP ****************
mod-Order: 8 | SNR (dB): 13.9
BER: 0.0009097525473071324
BLER: 0.5
Throughput: 60456000.0
.......................................................
**************** max-log-MAP ****************
mod-Order: 8 | SNR (dB): 13.9
BER: 0.007956199550086014
BLER: 0.875
Throughput: 15114000.0
.......................................................
************************************ Training the Model ***********************************
...........................................................................................
Epoch 1/4
24576/24576 [==============================] - 14s 563us/step - loss: 1.1139 - accuracy: 0.9612
Epoch 2/4
24576/24576 [==============================] - 15s 590us/step - loss: 0.0203 - accuracy: 0.9916
Epoch 3/4
24576/24576 [==============================] - 14s 576us/step - loss: 0.0152 - accuracy: 0.9931
Epoch 4/4
24576/24576 [==============================] - 13s 541us/step - loss: 0.0127 - accuracy: 0.9936
*********************************** Evaluating the Model **********************************
...........................................................................................
24576/24576 [==============================] - 11s 446us/step - loss: 0.0097 - accuracy: 0.9943
Training Accuracy: 99.43
498/498 [==============================] - 0s 398us/step
******************* LLRnet ******************
mod-Order: 8 | SNR (dB): 13.9
BER: 0.001091703056768559
BLER: 0.5
Throughput: 60456000.0
_______________________________________________________
+++++++++++ [ snrIndex: 2 | modorder: 8] +++++++++++
===================================================
**************** log-MAP ****************
mod-Order: 8 | SNR (dB): 14.4
BER: 0.0
BLER: 0.0
Throughput: 120912000.0
.......................................................
**************** max-log-MAP ****************
mod-Order: 8 | SNR (dB): 14.4
BER: 0.0
BLER: 0.0
Throughput: 120912000.0
.......................................................
************************************ Training the Model ***********************************
...........................................................................................
Epoch 1/4
24576/24576 [==============================] - 15s 579us/step - loss: 1.4182 - accuracy: 0.9590
Epoch 2/4
24576/24576 [==============================] - 14s 554us/step - loss: 0.0249 - accuracy: 0.9917
Epoch 3/4
24576/24576 [==============================] - 14s 571us/step - loss: 0.0212 - accuracy: 0.9928
Epoch 4/4
24576/24576 [==============================] - 14s 557us/step - loss: 0.0186 - accuracy: 0.9933
*********************************** Evaluating the Model **********************************
...........................................................................................
24576/24576 [==============================] - 11s 446us/step - loss: 0.0159 - accuracy: 0.9930
Training Accuracy: 99.30
498/498 [==============================] - 0s 395us/step
******************* LLRnet ******************
mod-Order: 8 | SNR (dB): 14.4
BER: 0.0
BLER: 0.0
Throughput: 120912000.0
_______________________________________________________
Performance Evaluation
Throughput vs SNR (dB) for 16-QAM, 64-QAM and, 256-QAM.
Throughput vs SNR (dB) for 16-QAM.
[12]:
fig, ax = plt.subplots()
ax.plot(SNRdB[0], Throughput[0,0]/10**6, 'mediumspringgreen', lw = 4, linestyle = "solid", marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "log-MAP")
ax.plot(SNRdB[0], Throughput[2,0]/10**6, 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X", ms = 9, mec = "green", mfc = "olive", label = "LLRnet")
ax.plot(SNRdB[0], Throughput[1,0]/10**6, 'tomato', lw = 3.5, linestyle = "dotted", marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "max-log-MAP")
ax.legend(loc="lower right")
ax.set_xlabel("SNR [dB]", fontsize = 9)
ax.set_ylabel("Throughput (Mbps)", fontsize = 9)
ax.set_title("Throughput vs SNR(dB)", fontsize = 12)
ax.set_ylim(0, maxThroughput[0]/10**6)
ax.set_xticks(SNRdB[0])
# Adding Twin Axes to plot using dataset_2
axr = ax.twinx()
axr.set_ylabel('Throughput [%]')
# axr.plot(x, dataset_2, color = color)
axr.set_ylim(0, 100)
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()
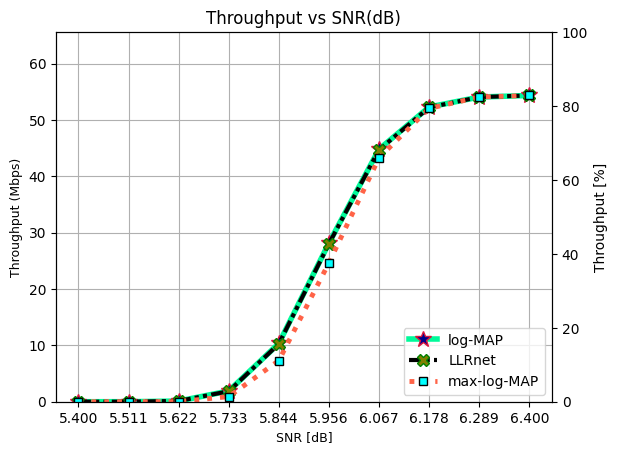
Throughput vs SNR (dB) for 64-QAM.
[14]:
fig, ax = plt.subplots()
ax.plot(SNRdB[1], Throughput[0,1]/10**6, 'mediumspringgreen', lw = 4, linestyle = "solid", marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "log-MAP")
ax.plot(SNRdB[1], Throughput[2,1]/10**6, 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X", ms = 9, mec = "green", mfc = "olive", label = "LLRnet")
ax.plot(SNRdB[1], Throughput[1,1]/10**6, 'tomato', lw = 3.5, linestyle = "dotted", marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "max-log-MAP")
ax.legend(loc="lower right")
ax.set_xlabel("SNR [dB]", fontsize = 9)
ax.set_ylabel("Throughput (Mbps)", fontsize = 9)
ax.set_title("Throughput vs SNR(dB)", fontsize = 12)
ax.set_ylim(0, maxThroughput[1]/10**6)
ax.set_xticks(SNRdB[1])
# Adding Twin Axes to plot using dataset_2
axr = ax.twinx()
axr.set_ylabel('Throughput [%]')
# axr.plot(x, dataset_2, color = color)
axr.set_ylim(0, 100)
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()
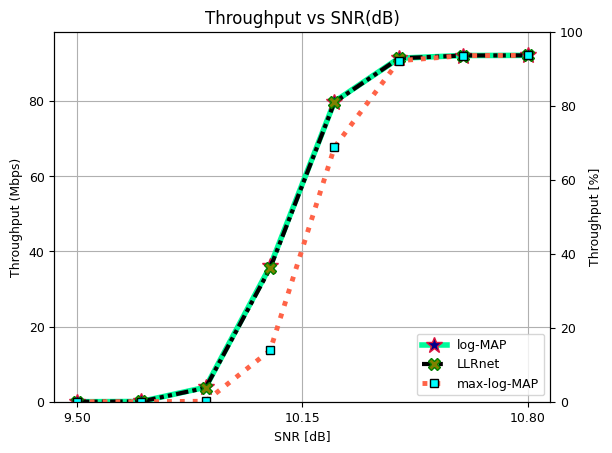
Throughput vs SNR (dB) for 256-QAM.
[15]:
fig, ax = plt.subplots()
ax.plot(SNRdB[2], Throughput[0,2]/10**6, 'mediumspringgreen', lw = 4, linestyle = "solid", marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "log-MAP")
ax.plot(SNRdB[2], Throughput[2,2]/10**6, 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X", ms = 9, mec = "green", mfc = "olive", label = "LLRnet")
ax.plot(SNRdB[2], Throughput[1,2]/10**6, 'tomato', lw = 3.5, linestyle = "dotted", marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "max-log-MAP")
ax.legend(loc="lower right")
ax.set_xlabel("SNR [dB]", fontsize = 9)
ax.set_ylabel("Throughput (Mbps)", fontsize = 9)
ax.set_title("Throughput vs SNR(dB)", fontsize = 12)
ax.set_ylim(0, maxThroughput[2]/10**6)
ax.set_xticks(SNRdB[2])
# Adding Twin Axes to plot using dataset_2
axr = ax.twinx()
axr.set_ylabel('Throughput [%]')
# axr.plot(x, dataset_2, color = color)
axr.set_ylim(0, 100)
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()
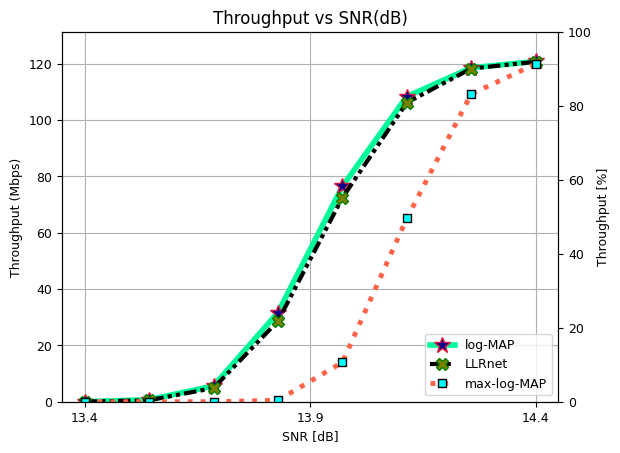
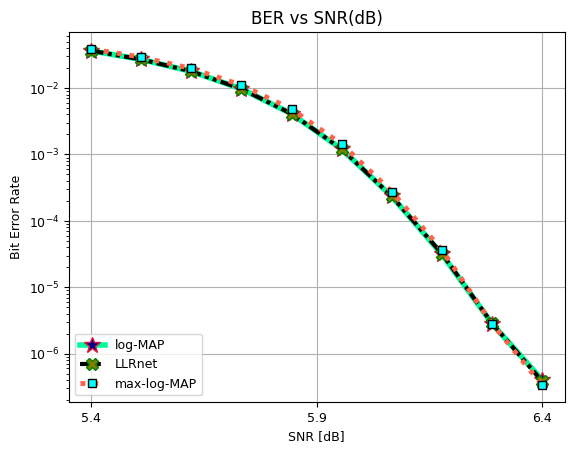
Bit Error rate (BER) vs SNR (dB) for 16-QAM, 64-QAM and, 256-QAM.
Comparison with:
max-log-MAP
log-MAP #### BER vs SNR for 16-QAM
[16]:
fig, ax = plt.subplots()
# BER for QAM-16
ax.semilogy(SNRdB[0], BER[0,0], 'mediumspringgreen', lw = 4, linestyle = "solid", marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "log-MAP")
ax.semilogy(SNRdB[0], BER[2,0], 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X", ms = 9, mec = "green", mfc = "olive", label = "LLRnet")
ax.semilogy(SNRdB[0], BER[1,0], 'tomato', lw = 3.5, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "max-log-MAP")
ax.legend(loc="lower left")
ax.set_xlabel("SNR [dB]", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("BER vs SNR(dB)", fontsize = 12)
ax.set_xticks(SNRdB[0])
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()
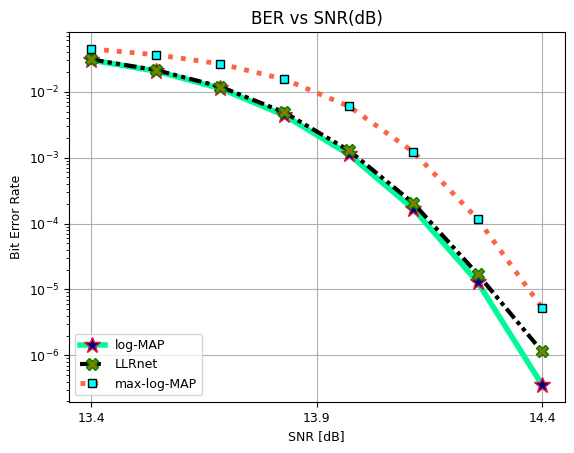
BER vs SNR for 64-QAM
[17]:
fig, ax = plt.subplots()
# BER for QAM-64
ax.semilogy(SNRdB[1], BER[0,1], 'mediumspringgreen', lw = 4, linestyle = "solid", marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "log-MAP")
ax.semilogy(SNRdB[1], BER[2,1], 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X", ms = 9, mec = "green", mfc = "olive", label = "LLRnet")
ax.semilogy(SNRdB[1], BER[1,1], 'tomato', lw = 3.5, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "max-log-MAP")
ax.legend(loc="lower left")
ax.set_xlabel("SNR [dB]", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("BER vs SNR(dB)", fontsize = 12)
ax.set_xticks(SNRdB[1])
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()
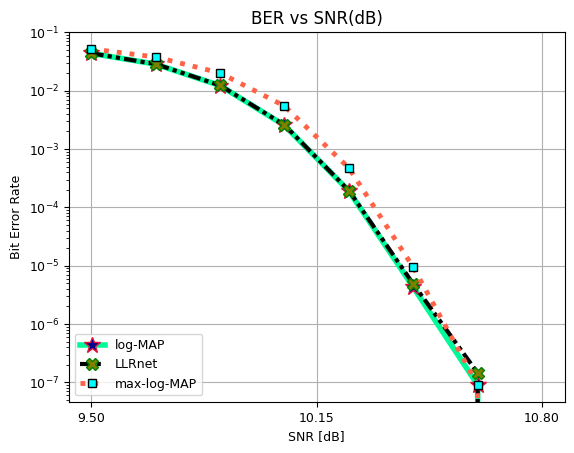
BER vs SNR for 256-QAM
[18]:
fig, ax = plt.subplots()
# BER for QAM-256
ax.semilogy(SNRdB[2], BER[0,2], 'mediumspringgreen', lw = 4, linestyle = "solid", marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "log-MAP")
ax.semilogy(SNRdB[2], BER[2,2], 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X", ms = 9, mec = "green", mfc = "olive", label = "LLRnet")
ax.semilogy(SNRdB[2], BER[1,2], 'tomato', lw = 3.5, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "max-log-MAP")
ax.legend(loc="lower left")
ax.set_xlabel("SNR [dB]", fontsize = 9)
ax.set_ylabel("Bit Error Rate", fontsize = 9)
ax.set_title("BER vs SNR(dB)", fontsize = 12)
ax.set_xticks(SNRdB[2])
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()
Block Error Rate (BLER) vs SNR (dB) for 16-QAM, 64-QAM and, 256-QAM.
Comparison with:
max-log-MAP
log-MAP
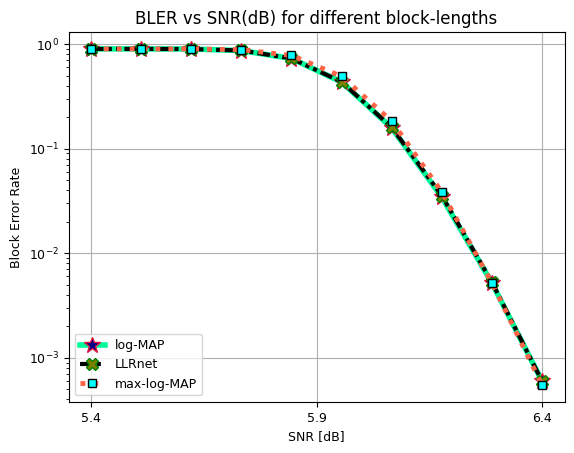
BLER vs SNR for 16-QAM
[19]:
fig, ax = plt.subplots()
# BER for QAM-16
ax.semilogy(SNRdB[0], BLER[0,0], 'mediumspringgreen', lw = 4, linestyle = "solid", marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "log-MAP")
ax.semilogy(SNRdB[0], BLER[2,0], 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X", ms = 9, mec = "green", mfc = "olive", label = "LLRnet")
ax.semilogy(SNRdB[0], BLER[1,0], 'tomato', lw = 3.5, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "max-log-MAP")
ax.legend(loc="lower left")
ax.set_xlabel("SNR [dB]", fontsize = 9)
ax.set_ylabel("Block Error Rate", fontsize = 9)
ax.set_title("BLER vs SNR(dB) for different block-lengths", fontsize = 12)
ax.set_xticks(SNRdB[0])
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()
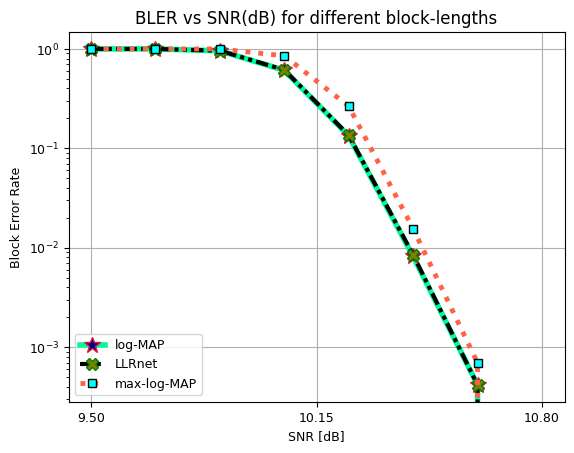
BLER vs SNR for 64-QAM
[20]:
fig, ax = plt.subplots()
# BER for QAM-64
ax.semilogy(SNRdB[1], BLER[0,1], 'mediumspringgreen', lw = 4, linestyle = "solid", marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "log-MAP")
ax.semilogy(SNRdB[1], BLER[2,1], 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X", ms = 9, mec = "green", mfc = "olive", label = "LLRnet")
ax.semilogy(SNRdB[1], BLER[1,1], 'tomato', lw = 3.5, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "max-log-MAP")
ax.legend(loc="lower left")
ax.set_xlabel("SNR [dB]", fontsize = 9)
ax.set_ylabel("Block Error Rate", fontsize = 9)
ax.set_title("BLER vs SNR(dB) for different block-lengths", fontsize = 12)
ax.set_xticks(SNRdB[1])
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()
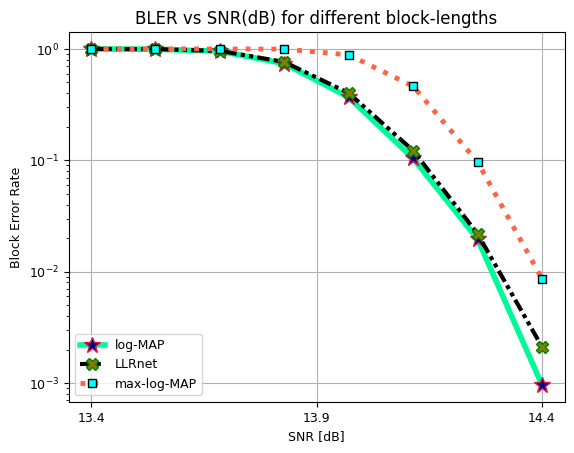
BLER vs SNR for 256-QAM
[21]:
fig, ax = plt.subplots()
# BER for QAM-256
ax.semilogy(SNRdB[2], BLER[0,2], 'mediumspringgreen', lw = 4, linestyle = "solid", marker = "*", ms = 12, mec = "crimson", mfc = "darkblue", label = "log-MAP")
ax.semilogy(SNRdB[2], BLER[2,2], 'k', lw = 3, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "X", ms = 9, mec = "green", mfc = "olive", label = "LLRnet")
ax.semilogy(SNRdB[2], BLER[1,2], 'tomato', lw = 3.5, linestyle = (0, (3, 1, 1, 1, 1, 1)), marker = "s", ms = 6, mec = "k", mfc = "cyan", label = "max-log-MAP")
ax.legend(loc="lower left")
ax.set_xlabel("SNR [dB]", fontsize = 9)
ax.set_ylabel("Block Error Rate", fontsize = 9)
ax.set_title("BLER vs SNR(dB) for different block-lengths", fontsize = 12)
ax.set_xticks(SNRdB[2])
plt.rcParams.update({'font.size': 9})
ax.grid()
plt.show()
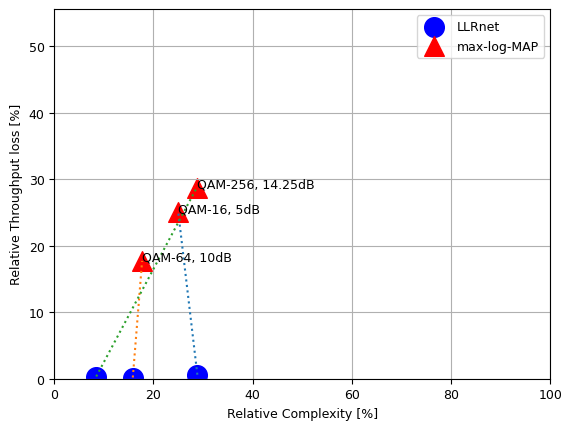
Complexity Analysis
Computational Complexity vs Throughput.
Computational Complexity vs BER/BLER.
Comparison with max-log-MAP and log-MAP.
Note: The throughput data used in following calculations is taken from the above simulations and the computational complexity number are provided by author in the paper. The complexity number for this paer may be slighlty different due to over configured model used for the simulation.
[22]:
complexityLogMAP = np.array([832, 3840, 17408])
complexityMaxLogMAP = np.array([208, 680, 5000])
complexityLLRnet = np.array([240, 608, 1472])
normalizedComplexityMaxLogMAP = complexityMaxLogMAP/complexityLogMAP*100
normalizedComplexityLLRnet = complexityLLRnet/complexityLogMAP*100
throughPutLogMAP = np.array([28.2, 60.05, 90.4]) # @ SNR (dB) = 5
throughPutMaxLogMAP = np.array([24.75, 42.12, 49.2]) # @ SNR (dB) = 10
throughPutLLRnet = np.array([28.03, 59.94, 90.1]) # @ SNR (dB) = 14.25
normalizedThroughPutMaxLogMAP = (1-throughPutMaxLogMAP/throughPutLogMAP)*100
normalizedThroughPutLLRnet = (1-throughPutLLRnet/throughPutLogMAP)*100
SNRdBValues = [5, 10, 14.25]
modOrder = [16,64,256]
fig, ax = plt.subplots()
ax.scatter(normalizedComplexityLLRnet, normalizedThroughPutLLRnet, marker = 'o', edgecolors="blue", facecolors="blue", s = 200, label = "LLRnet")
ax.scatter(normalizedComplexityMaxLogMAP, normalizedComplexityMaxLogMAP, marker = '^', edgecolors="red", facecolors="red", s = 200, label = "max-log-MAP")
for i in range(3):
plt.plot([normalizedComplexityLLRnet[i], normalizedComplexityMaxLogMAP[i]], [normalizedThroughPutLLRnet[i], normalizedComplexityMaxLogMAP[i]], ':')
plt.text(normalizedComplexityMaxLogMAP[i], normalizedComplexityMaxLogMAP[i],"QAM-"+str(modOrder[i])+", "+str(SNRdBValues[i])+"dB")
ax.set_xlabel("Relative Complexity [%]")
ax.set_ylabel("Relative Throughput loss [%]")
ax.set_xlim(0,100)
ax.set_ylim(0,normalizedThroughPutMaxLogMAP.max()+10)
ax.grid()
ax.legend()
plt.show()
Conclusion
Now that we have understood LLRnet, we are in a position to discuss the positives and the limitations of this model.
Positives of the LLRnet:
The positive of using LLRnet for decoding/demapping the equalized symbols are:
Low complexity and requires few samples for training.
Not impractical to train even online in real-time for demapping.
Limitations of the LLRnet:
On the other hand there are a few limitations of the techniques:
Robustness:
Performance is sensitive to estimate of SNR available.
Generalization:
Different models are required for different modulation orders.
Not generalized for all the SNRs.
Power consumption vs Cost:
Deployment of multiple models (for different modulation order and SNR) is computationally efficient but occupy large silicon (Si) space on FPGA or SoC.
Larger the silicon required, higher the cost and bulkier the device.
References:
Shental and J. Hoydis, “”Machine LLRning”: Learning to Softly Demodulate,” 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 2019, pp. 1-7, doi: 10.1109/GCWkshps45667.2019.9024433.
Python code for LLRNet.
[ ]: